Precalculus 5.5 Multiple-Angle and Product-Sum Formulas

5.5 Multiple-Angle and Product-Sum Formulas

Double Angle

A. Evaluating Functions Involving Double Angles:
Example 1:
Given: tan θ = 3/4, find cos 2θ

tan θ = opp/adj so therefore using Pythagorean theorem,
we know the hypotenuse is 5, so cos θ = 4/5

cos 2θ = 2 cos²θ - 1 = 2 (4/5)² - 1 = 2 (16/25) - 1 = .28 = 7/25

B. Solving a Multiple-Angle Equation
Example 2:
sin2x + cos x = 0

2 sin x cos x + cos x = 0

cos x (2 sin x + 1) = 0

Solving for x:

cos x = 0

x = π/2 , 3π/2

2 sin x + 1 = 0

sin x = - ½

x = 7π/6 and 11π/6

Therefore the general solution is

x = π/2 + π n and x = 7π/6 + π n


C. Power-Reducing Formulas

Power-Reducing/Half Angle Formulas

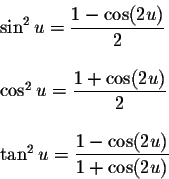
Example 3:

cos⁴ x = (cos²x)²




Product-to-Sum Formulas
sin u sin v = ½ (cos (u - v) - cos (u + v))
cos u cos v = ½ (cos (u - v) + cos (u + v))
sin u cos v = ½ (sin (u + v) + sin (u - v))
cos u sin v = ½ (sin (u + v) - sin (u - v))

Sum-to-Product Formulas




check out this web-site for additional help:
http://wps.prenhall.com/esm_blitzer_algtrig_2/0,7303,911519-,00.html