Geometry Chapter 4 - Congruence of line segments, angles, and triangles

Chapter 4 - Congruence of line segments, angles, and triangles - notes:
4-1 Postulates of lines, line segments, and angles –
Postulates:

4.1 A line segment can be extended to any length in either direction.
4.2 Through two given points, one and only one line can be drawn.
4.3 Two lines cannot intersect in more than one point.
4.4 One and only one circle can be drawn with any given point as it's center and the length of any given line segment as the radius.
4.5 At a given point on a given line, one and only one perpendicular can be drawn to the line.
4.6 From a given point not on a given line, one and only one perpendicular can be drawn to the line.
4.7 For any two distinct points, there is only one positive real number that is the length of the line segment joining the two endpoints.
4.8 The shortest distance between 2 points is the length of the line segment joining these two points.
4.9 A line segment has one and only one midpoint.
5.0 An angle has one and only one bisector.

4.2 Using Postulates and Definitions in Proofs:
We use the laws of logic to combine definitions and postulates to prove a theorem.
We will assume unless otherwise stated, that lines that appear to be straight lines in a figure actually are straight lines and that points that appear on the line actually are.

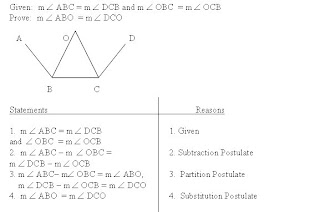
Example: Given: and AB = CD.
Prove: AC = BD
Statements Reasons
1. AB = CD 1. Given
2. BC = BC 2. Reflexive Postulate
3. AB + BC = CD + BC 3. Addition Postulate
4. AB + BC = AC; CD + BC = BD 4. partition postulate
5. AC = BD 5. Substitution postulate

4.3 Proving Theorems About Angles
Theorem 4.1 If 2 angles are right angles, then they are congruent.
Theorem 4.2 If two angles are straight angles, then they are congruent.

Definitions involving Pairs of Angles:

Definition:
Adjacent Angles are two angles in the same plane that have a common vertex and a common side but do not have any interior points in common.
Definition: Complementary angles are two angles, the sum of whose degree measure is 90 degrees.
Definition: Supplementary angles are two angles, the sum of whose degree measure is 180 degrees.
Theorem 4.3 If two angles are complements of the same angle or congruent angles, then the two angles are congruent.
Theorem 4.4 If two angle are congruent, then their complements are congruent.
Theorem 4.5 If two angles are supplements of the same angle, then they are congruent.
Theorem 4.6 If two angles are congruent, then their supplements are congruent.
If two angles are congruent, then they have the same supplement.

Definition: A linear pair of angles are two adjacent angles whose sum is a straight angle.
Theorem 4.7 If two angles form a linear pair, then they are supplementary.
Theorem 4.8 If two lines intersect to form congruent adjacent angles, then they are perpendicular.

Definition: Vertical angles are two angles in which the sides of one angle are opposite rays to the sides of the second angle.
Theorem 4.9: If two lines intersect, then the vertical angles are congruent.

How to present a proof in geometry using deductive reasoning.
1. As an aid, draw a figure that pictures the data of the theorem or the problem. Use letters to label points in the figure.
2. State the given, which is the hypothesis of the theorem, in terms of the figure.
3. State the Prove, which is the conclusion of the theorem, in terms of the figure.
4. Present the proof, which is a series of logical arguments used in the demonstration. Each step in the proof should consist of a statement about the figure. Each statement should be justified by the given, a definition, a postulate, or a previously proved theorem. The proof may be presented in a two-column format or in a paragraph form.

4.4 Congruent Polygons and Corresponding Parts
Corresponding Parts of Congruent Polygons


Two Polygons are congruent if and only if there is a one-to-one correspondence between their vertices such that corresponding angles are congruent and corresponding sides are congruent.
Therefore: Corresponding parts of congruent polygons are congruent.


















Congruent Triangles:
Corresponding parts of congruent triangles are congruent (CPCTC).

if two triangles are congruent, then the corresponding parts are congruent.












Postulates:
Reflexive Postulate: any geometric figure is congruent to itself.
Symmetric Postulate: a congruence may be expressed in either order.
Transitive Postulate: Two geometric figures congruent to the same geometric figure are congruent to each other.

4.5 - 4.7 Proving Triangles Congruent using
5 ways to show Triangle Congruence:

1. SAS = SAS Congruence Postulate - if two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the two triangles are congruent.Example: Given ΔABC and ΔDEF,if AB = DE, BC = EF and angle B = angle E, then ΔABC = ΔDEF.

2. SSS = SSS Congruence Postulate - if three sides of one triangle are congruent to three sides of a second triangle, then the two triangles are congruent.Example: Given ΔABC and ΔDEF,if AB = DE, BC = EF and AC = DF, then ΔABC = ΔDEF.

3. ASA = ASA Congruence Postulate - if two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the two triangles are congruent.Example: Given ΔABC and ΔDEF,if angle A = angle D, AB = DE, and angle B = angle E, then Δ ABC = Δ DEF.

4. AAS = AAS Congruence Postulate - if two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of a second triangle, then the two triangles are congruent.Example: Given Δ ABC and Δ DEF,if angle A = angle D, angle C = angle F, and BC = EF , then Δ ABC = Δ DEF.

5. HL = HL Congruence Postulate - if the leg and hypotenuse of one right triangle is congruent to the corresponding leg and hypotenuse of another right triangle, then the two triangles are congruent by hypotenuse - leg postulate.Example: Given right Δ ABC and right Δ DEF, if angle B and angle E are both right angles and leg AB = leg DE and hypotenuse AC = hypotenuse DF, then Δ ABC = Δ DEF.

Geometry Chapter 3 - Sections 3.5 - 3.8 - 2008 - 2009

3.5 - 3.8 Postulates, Theorems and Proof:


I. Postulate or axiom - a true obvious statement and accepted without proof.
- is a statement whose truth is accepted without proof.


II. Theorem - is a statement that is proved by deductive reasoning.


III. Postulates:


A. Reflexive Postulate: angle A = angle A : everything is congruent to itself

B. Symmetric Postulate: if angle A = angle B then angle B = angle A (somewhat like the converse)

C. The Substitution Postulate: a quantity may be substituted for its equal in any statement of equality.

Example: if x = y and y = 8, then we can conclude by substitution that x = 8.

D. Partition Postulate: a whole is equal to the sum of the parts (part + part = whole)

E. Addition Postulate: if a = b and c = d, then a + c = b + d

F. Subtraction Postulate: if a = b and c = d, then a - c = b - d

G. Multiplication Postulate: if a = b and c = d, then ac = bd

H. Division Postulate: if a = b and c = d, then a/c = b/d.

I. Power Postulate: if a = b then a² = b²

One of my students thought this would be a better way:

if a = b and c = d then a^c = b^d

Does anyone see a flaw in this?

J. Roots Postulate: if a = b and a is positive, then the square root of a = the square root of b



Example using a proof:

Chapter 3.4 Proofs

3 - 4 Direct Proofs: a proof that starts with the given statements and uses the laws of logic to arrive at the statement to be proved.

Examples we did in class:

Example1:

Example 2:

Example 3:

Example 4:

Example 5:

Unit 3 - Proving Statements in Geometry

Vocabulary - see blue sheet
A. Definitions:
1. Midpoint of a segment - divides it into two congruent segments.
2. Bisector of a segment or an angle - divides it into two congruent parts
3. Complementary Angles - are two angles whose sum is 90 degrees.
4. Supplementary Angles - are two angles whose sum is 180 degrees.
5. Perpendicular Lines - form right angles.
6. Perimeter of a polygon - is the sum of the lengths of the sides of a polygon.
7. Scalene triangle - has no congruent sides.
8. Isosceles Triangle - has at least two congruent sides.
9. Equilateral Triangle - has three congruent sides.
10. Altitude of a triangle - is a line drawn perpendicular from a vertex to the opposite side.
11. Median of a triangle - is a line drawn from a vertex to the midpoint of the opposite side and divides the opposite side into two congruent parts.
12. Parallelogram - is a quadrilateral with both pairs of opposite sides parallel.

B. Postulates:
1. Reflexive Postulate - any quantity is congruent to itself. angle A @ angle A
2. Transitivity Postulate - If angle A @ angle B, and angle B @ angle C, then angle A @ angle C.
3. Substitution Postulate - If angle A @ angle B, and angle A + angle C = 150 degrees, then by substitution, angle B + angle C = 150 degrees.
4. Partition Postulate - the part + the part = the whole. AB + BC = AC
5. Addition Postulate - If congruent quantities are added to congruent quantities, then their sums are congruent.
angle A @ angle B and angle C @ angle C, (angle C does not equal zero degrees)
then angle A + angle C = angle B + angle C.
6. Subtraction Postulate - If congruent quantities are subtracted from congruent quantities, then their differences are congruent.
angle A @ angle B and angle C @ angle C, (angle C does not equal zero degrees)
then Angle A - angle C = angle B - angle C.
7. Doubles Postulate - if two quantites are equal, then double their quantities are equal.
angle A = angle B, then 2(angle A) = 2(angle B).
8. Halves Postulate - if two quantities are equal, then half their quantities are equal.
angle A = angle B, then (1/2)(angle A) = (1/2)(angle B).

C. Theorems:
1. All right angles are congruent.
2. If two angles form a linear pair, then they are supplementary.
3. If two angles are supplements of the same angle, then they are congruent to each other.
3b. If two angles are complements of the same angle, then they are congruent to each other.
4. If two angles are congruent, then their supplements are congruent.
4b. If two angles are congruent, then their complements are congruent.
5. Vertical angles are congruent.
6. Corresponding parts of congruent triangles are congruent (CPCTC).
7. If two sides of a triangle are congruent, then the angles opposite are congruent.
7b. If two angles of a triangle are congruent, then the sides opposite are congruent.
8. An equilateral triangle is equiangular.
8b. An euqiangular triangle is equilateral.
9. If two lines form congruent adjacent angles, then the lines are perpendicular.
10 The supplement fo a right angle is a right angle.
11. If two lines are cut by a transversal forming congruent alternate interior angles, then the lines are parallel.
11b. If two lines are cut by a transversal forming congruent corresponding angles, then the lines are parallel.
11c. If two lines are cut by a transversal forming supplementary interior angles on the same side of the transversal, then then the lines are parallel.
11d. If two parallel lines are cut by a transversal, then the alternate interior angles are congruent.
11e. If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
11f. If two parallel lines are cut by a transversal, then the interior angles on the same side of the transversal are supplementary.
12. If two lines are perpendicular to the same line, then they are parallel.
13. If two lines are parallel to the same line, then they are also parallel.
14. Extensions and segments of parallel lines are parallel.
15. The sum of the measures of the interior angles of a triangle is 180 degrees.
16. The sum of the measures of the interior angles of a quadrilateral is 360 degrees.
17. The measure of the exterior angle of a triangle is equal to the sum of the two nonadjacent interior angles.
18. The sum of the measures of the interior angles of a polygon of n sides is 180(n - 2)
19. The measure of each interior angle of a regular polygon of n sides is (180(n-2))/n
20. The sum of the measures of the exterior angles of any polygon is 360 degrees.
21. The measure of each exterior angle of a regular polygon of n sides is 360/n.


3 - 1 Inductive Reasoning - uses a series of particular examples to lead to a general conclusion.

A. Inductive Reasoning is a powerful tool in discovering and making Conjectures - definition= generalizations arising from direct measurements of specific cases.

B. Care must be taken when applying inductive reasoning to ensure that all revelant examples are examined (no counterexample exists).

C. Inductive reasoning does not prove or explain the conjectures.


Based on these three triangles, what conjecture can you make about isosceles triangles?

Answer: If 2 sides of a triangle are congruent, then the opposite angles are congruent.


Example 2: Equilateral triangles - draw the 3 midpoints of the sides and connect them.
Make a conjecture about the 4 triangles that are formed.





Answer: It seems that it forms 4 congruent triangles

Example 3: If we draw parallelograms with opposite sides congruent by using both sides of the ruler, what conjectures can we form?

A. Opposite sides of a parallelogram are congruent.
B. It seems that all parallelograms have two acute angles and two obtuse angles.

The second conjecture is not true, if we make a parallelogram that is a rectangle, you can see all four angles are right angles, thus disproving conjecture B. This is called a counterexample - an example that shows the general conclusion is false.















You can see with 6 points, it should be 2^{6 - 1} = 2⁵ = 32 areas.

My students said that each time we added a point on the circle, it doubled the areas. They found out this is not true because they only had 30 or 31 areas.

In the left circle, there are 31 areas and in the right circle, there are only 30 areas. So this conjecture does not work.

This is why you have to be careful using inductive reasoning.


3 - 2 Deductive Reasoning
A. Deductive Reasoning - uses the laws of logic to combine definitions and general statements that we know to be true to reach a valid conclusion.

Every Good definition can be written as a true biconditional:

hypothesis if and only if conclusion

example:
Conditional statement: If a triangle has 2 congruent sides, then the angles opposite are congruent.

Converse: If a triangle has 2 congruent angles, then the sides opposite are congruent.

Since both the conditional and converse statements are true, then we can write the definition in biconditional form:

A triangle has 2 congruent sides if and only if the angles opposite are congruent.

Lets try another example:
Statement: A right triangle is a triangle with one right angle.

Conditional: If a triangle is a right triangle, then it has one right angle.
Converse: If a triangle has one right angle, then it is a right triangle.

Biconditional: A triangle is a right triangle if and only if it has one right angle.

3 - 3 Deductive Reasoning
1. A Proof in geometry is a valid argument that establishes the truth of a statement.
1. we use definitions, postulates and already proven theorems to show the truth of the statement.
Example: Recall the exercise with the equilateral triangle, we believed that it formed 4 congruent equilateral triangles. Using deductive reasoning, we can prove this conjecture to be true.




If 2 sides of a triangle are congruent, then the angles opposite are congruent. Each angle in an equilateral triangle measures 60 degrees so angle A = 60 degrees. That leaves angle AFB and angle BFA sum to be 180 - 60 = 120 degrees, (the sum of the angles in a triangle is 180 degrees). Since they are equal in measure, they each measure 60 degrees, forming a triangle with 3 angles measuring 60 degrees so this means it is an equiangular triangle (by definition of equiangular triangles) and equiangular triangles are equilateral triangles, so therefore each of the four triangles would have all three sides congruent (definition of equilateral triangle) forming 4 congruent equilateral triangles (all sides and angles are congruent).

How do we write a proof?

1. Two-Column Proof: has numbered statements and reasons that show the logivcal order of an argument.
2. Paragraph proof: a proof can be written in paragraph form. What we just did was a form of paragraph proof. You have to write the statements and give the reasons as part of your paragraph.
3. Flow proof: a chart that has arrows going from one statement to the next with the reasons written underneath the statement.

We will mainly use two-column proof:

Here are a few examples of algebraic proofs:








Just given some statement, we can conclude from the statement a new statement and have a reason for the statement.

Example:
Given: angle one and angle two are complementary, what can we conclude?
Conclusion: that the sum of angle one and angle two = 90 degrees by definition of complementary angles

Given: Ray BD bisects angle ABC
Conclusion: angle ABD is congruent to angle BDC by definition of angle bisector

Given: Line AB bisects line segment DE at point F
Conclusion: line segment DF is congruent to line segment FE by definition of segment bisector

Given: 0 is less than the measure of angle A which is less than 90 degrees.
Conclusion: angle A is an acute angle by definition of acute angle.

Given: B is between point A and C on line AC.
Conclusion: AB + BC = AC by partition postulate.

As you can see, you have been doing proofs, just not formally for awhile. We will continue these notes as we go along in our learning of proof writing. This is for a basic class in High School. There are many more ways to write proofs along with many more vocabulary words.

Geometry Chapter 2.5 - 2.8 Logic

Geometry chapter 2.5 Conditional Statements:

I) Vocabulary:
A. Conditional Statements - (if-then) - has two parts:

1. Hypothesis - (if)
2. Conclusion - (then)

Example: If it is noon in Georgia, then it is 9 am in California.

B) Converse Statement: Switch the hypothesis and conclusion of a Conditional Statement.

Example: If it is 9 am in California, then it is noon in Georgia.

C) Inverse Statement: negate both the hypothesis and conclusion of a Conditional Statement.

Example: If it is not noon in Georgia, then it is not 9 am in California.

1) Negation - write the negative of the statement.

Example: Statement: Angle A is acute.
Negation: Angle A is not acute or It is not true that angle A is acute.

D) Contrapositive Statement: Switch and negate both the Hypothesis and Conclusion of a Conditional Statement.

Example: If it is not 9 am in California, then it is not noon in Georgia.

E) Equivalent Statements: 2 statements that are both true or both false, they have the same truth value. Contrapositive statements is always equivalent to its Conditional statement. The converse statement is always equivalent to its inverse statement.

F) Counterexample: An example that shows that a conditional statement is false.

Example: If x² = 25, then x = 5

A counterexample is x = (-5) because (-5)² = 25 but 5 is not equal to (-5)

II) Postulates:

#5) Postulate 5: Through any 2 points there exists one line.
#6) Postulate 6: A line contains at least two points.
#7) Postulate 7: If two lines intersect, then their intersection is exactly one point.
#8) Postulate 8: Through any three noncollinear points there exists exactly one plane.
#9) Postulate 9: A plane contains at least three noncollinear points.
#10) Postulate 10: If two points lie in a plane, then the line containing them lies in the plane.
#11) Postulate 11: If two planes intersect, then their intersection is a line.

Geometry Chapter 2.6 Definitions and Biconditional Statements
I) Vocabulary:

A) Perpendicular: Two lines that intersect to form right angles.

B) Line Perpendicular to a Plane: A line that intersects a plane in a point and is perpendicular to every line that includes that point in the plane that intersects it.

C) Biconditional Statement: A statement that contains the words "if and only if" (iff) and is equivalent to writing a statement combining a conditional statement and its converse.

For the truth value of a biconditional statement to be true, both the conditional statemene and its converse have to have the same truth value.

Example: Conditional Statement: If two sides of a triangle are congruent, then the angles opposite them are congruent.
Converse Statement: If two angles of a triangle are congruent, then the sides opposite them are congruent.

Biconditional Statement: Two sides of a triangle are congruent if and only if the two angles of the triangle are congruent.

2.7 The Laws of logic -
patterns that are frequently used in drawing conclusions.

I. The law of Detachment -
A valid argument - uses a series of statements called premises that have known truth values to arrive at a conclusion.

If a conclusion is true (p → q ) and the hypothesis (p) is true, then the conclusion (q) is true.

Example: Given the following true statements, what can we conclude?
1. If adjacent angles are supplementary, then the angles form a linear pair.
2. Angle ABC and angle CBD are adjacent supplementary angles.

Conclusion: angle ABC and angle CBD form a linear pair.

II. The Law of Disjunctive Inference -
A. If a disjunction (p V q) is true and the disjunction (p) is false, then the other disjunction (q) has to be true.
B. If a disjunction (p V q) is true and the disjunction (q) is false, then the other disjunction (p) has to be true.

Example: Given the following true statements, what is a valid conclusion?
1. Paul is tall or Mort is short.
2. Paul is not tall.

Since Paul is not tall, so Mort has to be short.
Conclusion: Mort is short.

Example: Given the following true statements, what is a valid conclusion?
1. Carl listens to the radio or he cannot do his homework.
2. Carl cannot do his homework.

Since Carl cannot do his homework is true, then we have (p V true) is true. p could be either true or false so therefore:

Conclusion: No conclusion

Example: Given the following true statements, what sport does each person play?
1. Zach, Steve and David each play a different sport: basketball, soccer, or baseball. Zach made each of the following true statements:
2. I do not play basketball.
3. If Steve does not play soccer, then David plays baseball.
4. David does not play baseball.

What sport does each person play?
David does not play baseball. So therefore Steve does not play soccer is false for the 3rd statement to be true. This means that Steve does play soccer. This leaves David to play basketball and Zach to play baseball.

Example: Given the following true statements, which stock did Victoria sell yesterday?
1. Victoria owns stock in 3 companies: Alpha, Beta and Gamma.
2. Yesterday, Victoria sold her shares of Alpha or Gamma.
3. If she sold Alpha, then she bought more shares of Beta.
4. Victoria did not buy more shares of Beta.

Since Victoria did not buy more shares of Beta, then she did not sell Alpha. Since she did not sell Alpha, she had to sell her shares of Gamma.

Conclusion: She sold her shares of Gamma.

Chapter 2 Logic

Chapter 2 - Logic

Who are Leibniz, Boole, DeMorgan?

2 - 1 Sentences, Statements, and Truth Value

I. Logic - is the science of reasoning.
- help us to determine if a statement is true, false, or uncertain
- (the truth value of the statement)

The statements that we will use will be mathematic sentences

3 + 5 = 8 This is a true mathematical sentence

A midpoint of a line segment divides the line segment into 2 congruent parts.
This is a true mathematical sentence.

A pentagon is a six-sided polygon. This is a false mathematical sentence.

4 + 6 = 10. This is a false mathematical sentence.

II. Nonmathematical Sentences and Phrases
Sentences that do not state a fact, such as questions, commands, or exclamations
are not sentences that we use in the study of logic.

Example:

4 - 3 This is not a mathematical sentence

Go to your room! This is not a mathematical sentence.

III. Open Sentences - sentences that contain a variable.

Example:

x + 2 = 16 open sentence; variable is x

He ran the football in for a touchdown. open sentence; variable is he

17 - x = 9 open sentence; variable is x

Domain - is the input or the replacement set - the set of elements that are possible replacements for the variable.

Example:
x + 2 = 16 with the domain {5, 6, 7, 8, 9 }

Solution Set: the element or elements from the domain that make the open sentence true.

Therefore, the solution set is {8} because when x = 8, then 17 - 8 = 9 is true.

IV. Statement or closed sentence - can be judged to be true or false (no variables) - the truth value is either true (T) or false (F)

V. Negations of a statement always has the opposite truth value of the given statement.

Example: A frog is a snake. (This is a false statement).
Negation: A frog is not a snake. (This is a true statement).

Example: A triangle is not a polygon with 4 sides. (this is a true statement)
Negation: A triangle is a polygon with 4 sides. (this is a false statement)

to write this negation, you may have wanted to say:
A triangle is not not a polygon with 4 sides. As this doesn't make grammarical sense, we change the double negative to a positive.

VI. You can let a statement be represented by a lowercase letter.

Usually we use p, q, r, or s

If "p" is true, then not "p" or "~p" is false.

~p represents symbolically: not p.

Example:

Let p: Summer follows spring.

~p: Summer does not follow spring.

p is true so ~p is false

2 - 2 Conjunctions: is a compound statement formed by combining two simple statements using the word "and". From the table above, you see the symbol for and looks like an upside down V.

Example:

Let p: A dog is an animal.

Let q: A trumpet is a brass instrument.

What is the sentence for p and q?

A dog is an animal and a trumpet is a brass instrument.

What is the truth value for the following (we will negate the different parts of the sentence)

1. A dog is an animal and a trumpet is a brass instrument. (T and T = T)

2. A dog is an animal and a trumpet is not a brass instrument. (T and F = F)

3. A dog is not an animal and a trumpet is a brass instrument. (F and T = F)

4. A dog is not an animal and a trumpet is not a brass instrument. (F and F = F)

2 - 3 Disjunctions - is a compound statement formed by combining two simple statements using the word "OR" and the symbol for or is V.

Example:

Let p: January is the first month of the year.

Let q: Breakfast is a meal.

What is the sentence for p or q?

January is the first month of the year or breakfast is a meal.

What is the truth value for the following (we will again negate each part of the sentence)

January is the first month of the year or breakfast is a meal. (T or T = T)

January is the first month of the year or breakfast is not a meal. (T or F = T)

January is not the first month of the year or breakfast is a meal. (F or T = T)

January is not the first month of the year or breakfast is not a meal. (F or F = F)

Example:

Buffalo Bills is a football team.

Buffalo Sabres is a hockey team.

the or statement would be:

Buffalo Bills is a football team or Buffalo Sabres is a hockey team.

What is the truth value of this sentence?

True

Example:

Let our Set A = {1, 2, 3}

Set B = {2, 4, 6}

What is:

Set A V Set B = {1, 2, 3, 4, 6}

you include all the elements in both sets for "or"

Set A and Set B = {2}

you include only the elements that are in both set A and set B. This is what you called the intersection of the two sets.

I. Complement - is that which is not included in the set

Example:

the complement of Set A = {4, 6}

the complement of Set B = {1, 3}

II. Inclusive "or" - when we use the word "or" to mean that one or both of the simple sentences are true. This is the truth table we have used in this class.

2 - 4 Conditional - is a compound statement formed by using the words:

if ... then

symbolically: if p then q is p → q

"p" is the hypothesis or premise or antecedent

"q" is the conclusion or consequent

Example:

If today is Tuesday, then tomorrow is Wednesday.

Hypothesis: today is Tuesday

Conclusion: tomorrow is Wednesday

Other ways to write conditionals.

1. If today is Tuesday, then tomorrow is Wednesday.

2. Today is Tuesday implies that tomorrow is Wednesday.

3. When today is Tuesday, tomorrow is Wednesday.

Geometry - Chapter 1 - Essentials of Geometry

Chapter 1 - Essentials of Geometry

1-1 Undefined Terms:
A. Undefined terms: their meaning is accepted without definition
1. Point: definition - is that which has no part, a dot.
2. Set: is a collection of objects
3. Line - is breathless length;
4. Straight line: is a line that lies evenly with the points on itself.
5. Plane: is a set of points that form a flat surface extending indefinitely in all directions.

1-2 The real numbers and their Properties
B. Every real number corresponds to a point on a number line and every point on the number line corresponds to a real number.

1-3 Definitions, lines, and line segments

A. Definition: is a statement of the meaning of the term

B. Collinear set of points: is a set of points all of which lie on the same straight line.

C. Noncollinear set of points: is a set of three or more points that DO NOT all lie on the same straight line.

D. Distance between two points - every point on a line corresponds to a real number called its coordinate. To find the distance between any two points, find the absolute value of the difference between the coordinates of the two points.

If point A is at -2 and point D is at 1, what is the distance between A and D?

take the absolute value of (-2 - 1) = the absolute value of (-3) = 3

E. Order of points on a line
1. Betweenness: B is between A and C if and only if A, B, and C are distinct collinear points and AB + BC = AC

also, this is the partition postulate: the part + the part = the whole

2. Line Segment: or segment, is a set of points consisting of two endpoints on a line, called endpoints, and all of the points on the line between the endpoints.

1-5 Rays and Angles:

Definition: two points, A and B, are on one side of a point P if A, B, and P are collinear and P is not between A and B.

Half-line: every point on a line divides the line into 2 opposite set of points called half-lines.

Definition: A ray consists of a point (endpoint) on a line and all points on one side of the point.

Definition: Opposite rays: are two rays of the same line with a common endpoint and no other point in common.

Point B is the vertex, BA is a side of the angle and BC is the other side of the angle.

Definitions:

The measure of an angle is the number of degrees in the angle.

A straight angle is an angle that is the union of opposite rays.

Its degree measure is 180 degrees

Acute Angles - is an angle whose degree measure is greater than 0 degrees and less than 90 degres.

Right angles - is an angle whose degree measure is 90 degrees.

Obtuse angle - is an angle whose degree measure is greater than 90 degrees and less than 180 degrees.

Note:If you bisect a straight angle, you get two 90 degree angles or 2 right anglesIf you bisect an obtuse angle, you get two acute angles.

1-6 More angle definitions

Congruent angles are angles that have the same measure.

Definition: A bisector of an angle is a ray whose endpoint is the vertex of the angle and that divides that angle into two congruent angles.

Given angle ABC with angle bisector BD, we can conclude that angle ABD is congruent to angle CBD.

If angle ABC measures 70 degrees, what is the measure of angle ABD? 35 degrees

Example: Given angle QRS with angle bisector RT, if the measure of angle QRS = 10x, and the measure of angle SRT = 3x + 30, what is the measure of angle QRS?

we know: measure of angle QRT = measure of angle SRT + measure of angle QRS

and since the angle QRS is bisected by ray RT, then angle QRT = angle SRT

so 3x + 30 = measure of angle SRT,

therefore

3x + 30 + 3x + 30 = 10x

6x + 60 = 10x

60 = 4x

15 = x

measure of angle QRS = 10x = 10 (15) = 150 degrees

1-7 Triangles:

I) Vocabulary:

A) Base angles - the two angles adjacent to the base of an isosceles triangle.

B) Vertex angles - the angle opposite the base of an isosceles triangle.

II) Theorems:

A) Base Angles Theorem: if two sides of a triangle are congruent, then the angles opposite them are congruent.

B) Converse of the Base Angles Theorem: if two angles of a triangle are congruent, the the sides opposite them are congruent.

Corollaries:

A) If a triangle is equilateral, then it is equiangular.

B) If a triangle is equiangular, then it is equilateral.

I) Vocabulary:

A) Triangle - is a figure formed by three segments joining three noncollinear points.

B) Classification of triangles:

1) By sides:

a) Equilateral Triangle - has 3 congruent sides

b) Isosceles Triangle - has at least 2 congruent sides

c) Scalene Triangle - has no congruent sides

2) By angles:

a) Acute Triangle - has 3 acute angles

b) Equiangular Triangle - has 3 congruent angles that measure 60 degrees each

c) Right Triangle - has one right angle and 2 acute angles

d) Obtuse Triangle - has one obtuse angle and 2 acute angles

C) Vertex - each of the three points joining the sides of a triangle (plural - vertices)

D) Adjacent Sides - in a triangle, two sides sharing a common vertex.

E) Right triangles have 2 sides that form the right angle called the legs. The side opposite the right angle is the hypotenuse of the triangle.

F) Interior angles - when the sides of a triangle are extended, other angles are formed. the three original angles are the interior angles.

G) Exterior angles - the angles that are adjacent to the interior angles.

H) Theorem:

1) Triangle sum theorem - the sum of the measures of the interior angles of a triangle is 180 degrees.

2) Exterior Angle Theorem - the measure of an exterior angle of a triangle is equal to the sum of the measures of the two nonadjacent interior angles.

I) Corollary to a theorem - is a statement that can be proved easily using the theorem.

Example: The acute angles of a right triangle are complementary.

Example: given Triangle ABC with side BC extended through point D, if angle A = 65 degrees and angle ACD = 2x + 10 and angle B = x, solve for x.
angle A + angle B = angle ACD65 + x = 2x + 1055 = x

Geometry - Similar Triangle Proofs

Similar Triangle Proofs:

If 2 angles of one triangle are congruent to two corresponding angles of a second triangle, then the third angles are congruent.

There are 3 ways to show triangle similarity:



Let's try a proof:

Let's try another:

Geometry HW #14

For my Geometry Class: here is homework #14, questions 1 & 2 Quadrilateral Proofs

Quadrialteral Properties

Quadrilateral "Family Tree" -

Quadrilateral - 4 sided polygon

A. Kite -
1. has consecutive sides congruent but opposite sides are not.
2. the diagonals are perpendicular
3. has exactly one pair of opposite angles congruent.

B. Trapezoid -
1. Has exactly one pair of opposite sides parallel

C. Isosceles Trapezoid -
1. Has exactly one pair of opposite sides parallel
2. the non-parallel sides are congruent (legs congruent)
3. the diagonals are congruent
4. the base angles are congruent

D. Parallelogram -
1. Definition: has both pairs of opposite sides parallel
2. has both pairs of opposite sides congruent
3. has one pair of opposite sides parallel and congruent
4. has both pairs of opposite angles congruent
5. has consecutive angles supplementary
6. the diagonals bisect each other
7. the diagonals divide the parallelogram into 2 congruent triangles

E. Rhombus -
1. All of the properties of a parallelogram
2. All sides are congruent (equilateral)
3. diagonals are perpendicular
4. diagonals bisect opposite angles

F. Rectangle -
1. All of the properties of a parallelogram
2. all angles are congruent (equiangular)
3. diagonals are congruent

G. Square -
1. All the properties of a parallelogram, rhombus and rectangle

check out this website:
http://regentsprep.org/Regents/math/quad/LQuad.htm

Coordinate Geometry

Geometry - Coordinate Geometry:

check out this website:
http://regentsprep.org/Regents/mathb/1D/Coordinatelesson.htm

B(x₁, y₁) and A (x₂, y₂) is from the
Pythagorean Theorem which is:

c² = a² + b²

since a = (x₂ – x₁) and b = (y₂ – y₁)

we get

c² = (x₂ – x₁)² + (y₂ – y₁)²
so taking the square root of both sides we have our distance formula.

Here are the Slope Formula and the Midpoint Formula:

Using the following chart, if we have to prove congruent segments, we have to show they have equal length by using the distance formula.

Here is a web-site to hopefully help:

http://library.thinkquest.org/20991/geo/coordgeo.html

Geometry Proofs - unit 2 Triangles

Triangles – Proofs – Unit 2
1. Δ ABC is congruent to Δ ABC , this is by the Reflexive Postulate
2. if Δ ABC is congruent to Δ DEF then Δ DEF is congruent to Δ ABC, this is by the Symmetric Postulate
3. if Δ ABC is congruent to Δ DEF and Δ DEF is congruent to Δ GHI, Then Δ ABC is congruent to Δ GHI by the Transitivity Postulate

5 ways to show Triangle Congruence:
1. SAS = SAS Congruence Postulate - if two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the two triangles are congruent.
Example: Given ΔABC and ΔDEF,
if AB = DE, BC = EF and angle B = angle E, then ΔABC = ΔDEF.

2. SSS = SSS Congruence Postulate - if three sides of one triangle are congruent to three sides of a second triangle, then the two triangles are congruent.
Example: Given ΔABC and ΔDEF,
if AB = DE, BC = EF and AC = DF, then ΔABC = ΔDEF.

3. ASA = ASA Congruence Postulate - if two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the two triangles are congruent.
Example: Given ΔABC and ΔDEF,
if angle A = angle D, AB = DE, and angle B = angle E, then Δ ABC = Δ DEF.

4. AAS = AAS Congruence Postulate - if two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of a second triangle, then the two triangles are congruent.
Example: Given Δ ABC and Δ DEF,
if angle A = angle D, angle C = angle F, and BC = EF , then Δ ABC = Δ DEF.

5. HL = HL Congruence Postulate - if the leg and hypotenuse of one right triangle is congruent to the corresponding leg and hypotenuse of another right triangle, then the two triangles are congruent by hypotenuse - leg postulate.
Example: Given right Δ ABC and right Δ DEF, if angle B and angle E are both right angles and leg AB = leg DE and hypotenuse AC = hypotenuse DF, then Δ ABC = Δ DEF.

I) Vocabulary:
A) When two figures are congruent, there is a correspondence between their angles and sides such that corresponding angles are congruent and corresponding sides are congruent.
Example: Given Δ ABC is congruent to Δ PQR then we know
1) angle A = angle P, angle B = angle Q, and angle C = angle R
2) AB = PQ, BC = QR, and AC = PR By Corresponding Parts of Congruent Triangles are Congruent (CPCTC) - which means that if 2 triangles are congruent, then their corresponding parts are congruent

Make sure that you list the corresponding angles in the same order with the triangle congruence.
Example: ΔABC = ΔDEF is not the same as ΔABC = ΔEFD because
ΔABC = ΔDEF has angle A = angle D, angle B = angle E and angle C = angle F
while ΔABC = ΔEFD has angle A = angle E, angle B = angle F and angle C = angle D

B) Third Angles Theorem - if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.

C) Reflexive Postulate - Every triangle is congruent to itself

D) Symmetric Postulate - If ΔABC = ΔDEF, then ΔDEF = ΔABC

E) Transitive Postulate - If ΔABC = ΔDEF and ΔDEF = ΔJKL, then ΔABC = ΔJKL

Theorems to remember:

If 2 angles of one triangle are congruent then the sides opposite are congruent.
If 2 sides of one triangle are congruent then the angles opposite are congruent.
________________________________________________________________
Practice Proofs:

Precalculus Unit 8 - chapter 6.3, 6.4, 10.5, 10.6, 10.7

PRECALCULUS
Unit 8
Vectors and Parametric/Polar Equations

Section 6.3A HW# 53; Pg.453; #1 – 45 by 4’s (1, 5, 9, …)

Section 6.3B; HW # 54; *Pg.453; #3, 11, 19, 23, 31, 39, 43
Pg.454; #49, 53, 57, 61, 65, 69, 73, 74, 82

Section 6.4; HW # 55; *Pg. 454; #51, 55, 59, 63, 67, 71,
Pg. 464; #1, 5, 9, 13, 17, 21, 25, 29, 33, 37
Quiz on Sections 6.3A – 6.3B Next Class

Section 10.5; HW# 56; *Pg.464; #3, 7, 11, 15, 19, 23, 27, 31
Pg.736; #1, 5, 9, 13, 21, 29, 41, 47

Section 10.6; HW# 57; *Pg.736; #3, 7, 11, 17, 27, 43
Pg.743; #5 – 41 by 4’s, 45, 50, 53 – 57 odds
Quiz on Sections 6.4 – 10.5 Next Class

Section 10.7; HW# 58; *Pg.743; #7, 11, 15, 23, 27, 39, 47, 59
Pg.752; #21 – 33 odds, 55, 59

Review HW #59
Pg.480; 39, 43, 47, 51, 59, 69, 79, 83, 85
Pg.762; 47, 49, 59, 65, 69, 73, 75, 81, 85, 89

HW #60; Unit 8 Test

Unit One for Proofs - Angles and Lines

The addition Postulate:

If a = b and c = d, then a + c = b + d

The Partition Postulate:

AB + BC = AC

These are two different concepts. Let's try a proof:

As you can see, in step 2, we added equal quantities to each other. This is Addition Postulate.

But in step 3, we added a part plus a part equals a whole so this is Partition.

Let's try another example:

Here we used the Subtraction Postulate: subtracting equal quantities from equal quantities.

In step 3, we had the whole minus a part equals a part. This is still Partition Postulate.

Geometry Vocabulary for Proofs

Vocabulary - Euclidean Geometry:

1. Space - is a set of points that forms a completely flat surface extending indefinitely in all directions.

2. Collinear Points - is a set of points all of which lie on the same straight line.

3. Coplanar points - is a set of points all of which lie on the same plane.

4. Betweenness of Points or Segment/Angle Addition Postulate (we will call this Partition Postulate) - point B is between point A and point C, if A, B and C are distinct collinear points and AB + BC = AC. We shall say that the part plus the part equals the whole (part + part = whole)

5. Segment or line segment - is a set of points consisting of two points on a line, called endpoints, and all the points on the line between the endpoints.

6. Length of a line segment - is the distance between the endpoints.

7. Congruent segments - are segments that have the same measure.

Congruent angles - are angles that have the same measure.

8. Midpoint of a segment - is the point of the line segment that divides the segment into two congruent segments or divides the line segment in half.

9. Bisector of a Segment or angle - is any line, ray, or point that intersects the segment or angle at its midpoint.

10. Rays - is a part of a line that consists of a point on the line called the endpoint and all the points on one side of the endpoint

11. Opposite Rays - are two rays of the same line with a common endpoint and no other point in common.

12. Angle - is a set of points that is the union of two rays having the same endpoint or vertex.

13. Sides of an angle - are the rays that make up the angle

14. Vertex of an angle - is the common endpoint of the two sides of an angle.

15. Adjacent angles - are two angle in the same plane that have a common vertex and a common side but do not have any common interior points.

16. Exterior sides of adjacent angles - the two sides of adjacent angles that are not common to both angles.

17. Vertical angles - are two angles in which the sides of one angle are opposite rays to the sides of the second angle. Vertical angles are congruent.

18. Addition Postulate - if A = B, then A + C = B + C

19. Subtraction Postulate - if A = B, then A - C = B - C

20. Multiplication Postulate - if A = B, then AC = BC

21. Division Postulate - if A = B and C does not equal zero, then A/C = B/C

22. Halves Postulate - if A = B, then A/2 = B/2

23. Doubles Postulate - if A = B, then 2A = 2B

24. Substitution Postulate - if A = 5 and A + B = 12, then 5 + B = 12.

- you plug in the equal value

25. Reflexive Postulate - A = A

26. Symmetric Postulate - if A = B, then B = A.

27. Transitivity Postulate - if A = B AND B = C, then A = C

OR if A is less than B AND B is less than C, then A is less than C.

28. Distributive Postulate - if A(B + C) then AB + AC

Other Vocabulary:

Congruent Angles - angles that have the same measure.

Complementary Angles - are two angles that the sum of their measures is 90 degrees

Supplementary Angles - are two angles that the sum of their measures is 180 degrees.

Perpendicular Lines - form right angles.

Right angle - has a measure of 90 degrees.

Linear pair - are two adjacent angles where their noncommon side are opposite rays.

Here is one way how to write a proof:

1. You set up a t-table and write the word Statements in the left column and Reasons in the right column.

2. You are given a statement with another statement to prove based on the given statement.

3. You write the given statement in the left column with the word given for your reason. Then you write statements that support what you are given with logically reason using vocabulary, postulates or already proven theorems.

Here are a few examples of algebraic proofs:

As you can see, you have been doing proofs, just not formally for awhile. We will continue these notes as we go along in our learning of proof writing. This is for a basic class in High School. There are many more ways to write proofs along with many more vocabulary words.

Precalculus Midterm Requirements

Requirements for Midterm:

Do 3 of the 6 projects from Chapters: Prerequisite, One, Two, Three, Four, or Five
These can be found at the end of each of the chapters.
Handwritten is fine. If you type the project out, one extra credit point per problem.
Show all work!! No work, no credit. Each question is worth 15 points.

Total points for midterm: 45 points.

The projects can be found on the following pages:
Prerequisite, page 70
Chapter 1, page 133
Chapter 2, page 213
Chapter 3, page 279
Chapter 4, page 373
Chapter 5, page 425

Answer all of the questions for each project chosen.