Precalculus 1.5 Inverse Functions:
I. Inverse Functions:
A. Let "f " and "g" be two functions such that
f (g(x)) = x for every "x" in the domain of "g"
and
g( f (x)) = x for every "x" in the domain of "f ".
Under these conditions, the function "g" is the INVERSE of the function "f ":
The function "g" is denoted by f -1 (read f-inverse), so:
f ( f -1(x)) = x
AND
f -1( f (x)) = x
The domain of "f " must be equal to the range of f -1
AND
the range of "f " must be equal to the domain of f -1
Example:
Given f (x) = {(1,2), (4,5), (6,7)}
then f -1 (x) = {(2,1), (5,4), (7,6)}
The graphs of "f " and "f -1 are related to each other by the fact the graph of "f -1" is a reflection of the graph of "f " in the line y = x.
Example:
If the function f has values: {(1,0), (2,3), (4,7)}
then f -1 has values of {(0,1), (3,2), (7,4)}
Example:
Find the inverse of f (x) = 4x + 8
1. let f (x) = y, so by substitution we get
y = 4x + 8
2. Switch the x and y
x = 4y + 8
3. Solve for y
x - 8 = 4y
(1/4) x - 2 = y
4. Now y = f -1 so
f -1 = (1/4) x - 2
Example: Show that f(x) = (x + 8)/3 and g(x) = 3x - 8 are inverse functions of each other. Recall that f(g(x)) = x and g(f(x)) = x therefore:
f (g (x)) = ( (3x-8)+8)/ 3 = (3x)/3 = x so f(g(x)) = x
g ( f (x)) = 3((x + 8)/3) - 8 = x + 8 - 8 = x so g (f (x)) = x
so these two functions are inverse functions of each other.
Example: Find the inverse function of f (x) = x3+5
1. y = x3 + 5
2. x = y3 + 5
3. x - 5 = y3
(x - 5)1/3 = y
so
f -1(x) = (x - 5)1/3
Check answer:
f (f -1(x)) = x
((x - 5)1/3)3 + 5 = x - 5 + 5 = x so it checks
II. One - to - one function:
A function is one-to-one if, for "a" and "b" in the domain
f (a) = f (b) implies that a = b.
A function "f " has an inverse function " f " if and only if " f " is one-to-one.
Use the horizontal line test to check if a function is one-to-one. If the equation can have a horizontal line pass through it only once at any value, then the function is one-to-one.
Example: y2 = x,
doing the vertical line test (to see if it is a function) you see that when x = 1, y = -1 or y = 1 so
this is not a function
but by using the horizontal line test, the line never hits twice so therefore this equation has a one-to-one relationship.
Example: y = x3
this is a function and it has a one-to-one relationship so therefore
this is a one-to-one function.
Testing for One-to-one Functions:
If the function f (x) = x3 + 7
Show that f (a) = f (b)
a3 + 7 = b3 + 7
a3 = b3
a = b so yes it is.
Example:
g (x) = 5x2 + 8
5 (a)2 + 8 = 5 (b)2 +8
5a2 = 5b2
a2 = b2
so you could get:
a = b or
-a = b or
a = -b or
-a = -b
so therefore this function is not one-to-one.
Wednesday, September 26, 2007
Precalculus 1.2b Graphs of Functions
Precalculus 1.2 b Graphs of functions:
I. to graph a piece-wise function:
Given:
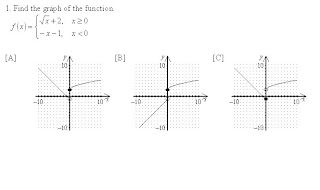
So to find the answer to this, find f(0).
Since 0 is equal to 0, we would use the first function.
so f(0) = √0 + 2 = 2, this means it is a solid dot at (0, 2) so the answer cannot be C.
and it is an open dot at f(0) = -x - 1 = -1 because it does not equal zero here.
Now we look at the graph of each function.
f(x) = -x - 1 has a negative slope so the answer would be A.
A way to check your answer is by using your graphing utility.
In y1 = (√ x + 2)(x≥0)
In y2 = (- x - 1)(x is less than 0)
with this you can see that the graph could be A or C. Now using your table, you can see that
y1 = 2 where y2 = 0 (this zero means no - the function doesn't exist here) so this means that
y1 would be a solid dot and y2 is open.
II. Even Function:
A function f is even if, for each x in the domain of f, f (-x) = f (x)
Example:
f (x) = x2 + 4
Test the function:
1st - Is it a function - yes it is
2nd - does f (-x) = f (x)
f (-x) = (-x)2 + 4
= x2 + 4
Therefore: f (-x) = x2 + 4 and
f (x) = x2 so
f (-x) = f (x) so this function is even.
III. Odd Function
A function f is odd if, for each x in the domain of f,
f (-x) = - f (x)
Example:
f(x) = x5 - x3
f(-x) = (-x)5 - (-x)3
= -x5 - - x3
= - (x5 - x3)
-f(x) = - (x5 - x3) so...
f (-x) = - f(x) so this function is odd.
IV. Neither an Even Function or Odd Function
A function f is neither if, for each x in the domain of f
a) f (-x) ≠ f (x) AND
b) f (-x) ≠ - f(x)
Example:
f (x) = 5 - 3x
f (-x) = 5 - 3(-x) = 5 + 3x
-f(x) = - (5 - 3x) = -5 + 3x
so since f (x) ≠ f (-x) and
f (-x) ≠ - f(x), this function is neither even or odd
V. Graphically showing even, odd or neither functions:

I. to graph a piece-wise function:
Given:

So to find the answer to this, find f(0).
Since 0 is equal to 0, we would use the first function.
so f(0) = √0 + 2 = 2, this means it is a solid dot at (0, 2) so the answer cannot be C.
and it is an open dot at f(0) = -x - 1 = -1 because it does not equal zero here.
Now we look at the graph of each function.
f(x) = -x - 1 has a negative slope so the answer would be A.
A way to check your answer is by using your graphing utility.
In y1 = (√ x + 2)(x≥0)
In y2 = (- x - 1)(x is less than 0)
with this you can see that the graph could be A or C. Now using your table, you can see that
y1 = 2 where y2 = 0 (this zero means no - the function doesn't exist here) so this means that
y1 would be a solid dot and y2 is open.
II. Even Function:
A function f is even if, for each x in the domain of f, f (-x) = f (x)
Example:
f (x) = x2 + 4
Test the function:
1st - Is it a function - yes it is
2nd - does f (-x) = f (x)
f (-x) = (-x)2 + 4
= x2 + 4
Therefore: f (-x) = x2 + 4 and
f (x) = x2 so
f (-x) = f (x) so this function is even.
III. Odd Function
A function f is odd if, for each x in the domain of f,
f (-x) = - f (x)
Example:
f(x) = x5 - x3
f(-x) = (-x)5 - (-x)3
= -x5 - - x3
= - (x5 - x3)
-f(x) = - (x5 - x3) so...
f (-x) = - f(x) so this function is odd.
IV. Neither an Even Function or Odd Function
A function f is neither if, for each x in the domain of f
a) f (-x) ≠ f (x) AND
b) f (-x) ≠ - f(x)
Example:
f (x) = 5 - 3x
f (-x) = 5 - 3(-x) = 5 + 3x
-f(x) = - (5 - 3x) = -5 + 3x
so since f (x) ≠ f (-x) and
f (-x) ≠ - f(x), this function is neither even or odd
V. Graphically showing even, odd or neither functions:
1. A function whose graph is symmetric with respect to the y-axis is an even function.
2. A function whose graph is symmetric with respect to the origin is an odd function.
3. A function whose graph is not symmetric with respect to the y-axis or the origin is a neither function.
Example:
Can you figure out which of these graphs are even, odd or neither?

1. Graph A is neither because it is not symmetric to the y-axis or the origin.
2. Graph B is an even function because it is symmetric to the y-axis.
3. Graph C is an odd function because it is symmetric to the origin.
VI. The Greatest Interger Function:
is denoted by [[x]] and is defined by
f (x) = [[x]] = the greatest integer less than or equal to x.
The graph of the greatest integer function jumps vertically one unit at each integer and is contant (a horizontal line segment) between each pair of consecutive integers.
Example: f (x) = [[x]]
[[-2]] = -2
[[-1.5]] = -2
[[-0.5]] = -1
[[1.5]] = 1
From this you can see that the value of the x rounded down to the nearest integer.
To put this on the graphing utility:
y1 = math → num↓#5 int( x)
Example 2:
f (-4) = [[-1]] - 2 = -1 - 2 = -3
f (-3.5) = [[-.875]] - 2 = -1 - 2 = -3
So we can definitely throw C away. So looking at A or B,
and since f (-4) = -3, this means the dot is closed so the answer would be A.
Precalculus 2.2 Polynomial Functions of Higher Degree
Precalculus 2.2 Polynomial Functions of Higher Degree
You can find extra notes at the following website:
http://scidiv.bcc.ctc.edu/FL/MATH105/sso0202.pdf
I. Graphs of:
Polynomial functions are continuous if -
they have no breaks, holes, or gaps.
Example 1: This graph is continuous
Example 2: Piece-wise functions are not continuous
II. Simple Graphs:
f (x) = xn, where n is greater than zero
1. If n is even, the graph of y = xn touches the axis at the x-intercept.
2. If n is odd, the graph of y = xn crosses the axis at the x-intercept.
III. The Leading Coefficient Test
Given f(x) = anxn + ... + a1x + a0
1. When "n" is odd:
a. If the Leading Coefficient is positive (an is greater than 0), the graph falls to the left and rises to the right.
b. If the Leading Coefficient is negative (an is less than 0), the graph rises to the left and falls to the right.
2. When "n" is even:
a. If the Leading Coefficient is positive (an is greater than 0), the graph rises to the left and right.
b. If the Leading Coefficient is negative (an is less than 0), the graph falls to the left and right.
*This determines ONLY the right and left behavior of the graph!
IV. Zeros of Polynomial Functions:
1. The graph of "f" has at most "n" real zeros.
2. The function has at most n-1 relative extrema (relative minimum or maximums).
Example: Given y = x2
n = 2
so
2 real zeros and (n-1) or 1 minimum
V. Real Zeros:
1. x = a is a zero of the function "f"
2. x = a is a solution of the polynomial equation f (x) = 0
3. (x - a) is a factor of the polynomial f (x)
4. (a, 0) is an x-intercept of the graph of "f".
Example: f (x) = x2 - 8x + 15
0 = x2 - 8x + 15
0 = (x - 5)(x - 3)
x = 5 and x = 3
therefore the zeros are (5, 0) and (3, 0)
x2 so n = 2 so ... there are at least 2 real zeros
graph: a is greater than 0 so this function rises to the left and right.
Example: f (x) = (-3/8) x4 - x3 + 2x2 + 5
Given the zeros:
1. Leading Coefficient = -3/8
2. Leading Degree is 4 so it is even
Therefore the graph falls to the left and the right.
Note: use the calculator to find the intercepts if algebraically not able to at this stage
When you graph the above function:
Maximum: (-2.914851686, 19.68779879)
Zeros: (-4.141946129, 0) and (1.934035914, 0)
Example: f (x) = x3 - 4x
Leading Coefficient = 1
Leading degree is 3 so it is odd
The graph falls to left and rises to the right
0 = x3 - 4x
0 = x (x2 - 4)
0 = x (x + 2)(x - 2)
0 = x, x = -2, and x = 2
Maximum value (-1.15, 3.08)
Minimum value (1.15, -3.08)
VI. Multiplicity for the Factor (x - r)k
In general, a factor of (x - r)k yields a repeated zero x = r of multiplicity k.
1. If k is odd, the graph crosses the x-axis at x = r
2. If k is even, the graph touches (but does not cross) the x-axis at x = r.
Example: f (x) = 4x2 -6x + 9
Find all zeros:
0 = 4x2 - 6x + 9
0 = (2x - 3)(2x - 3)
0 = (2x - 3)2
so we know a zero is (3, 0)
Using #2 above, k = 2 so it is even, therefore the graph touches the x-axis at x = 3
Example 2: Find the x-intercepts and multiplicity of f (x) = 2(x + 2)2(x - 3)
x-intercepts are (-2, 0) and (3, 0) and the mutiplicity of 2.
2.2b Finding a Polynomial with Given Zeros:
I. Finding a Polynomial with given zeros
Example 1: given zeros: -4 and 5
1. For each of the given zeros, form a corresponding factor.
We have: x = -4 and x = 5
f (x) = (x + 4)(x - 5)
= x2 - 5x + 4x - 20
= x2 - x - 20
Now sketch the graph:
1. Apply the Leading Coefficient test
Leading Coefficient is 1 and 1 is positive and the degree is 2 so it is even
Therefore the graph rises to the left and right.
2. Use zeros given: (-4, 0) and (5, 0)
3. Find the y-intercept by letting x = 0
f (0) = -20
4. Find the vertex
x = -b/(2a) = 1/2
f (1/2) = -20.25
So now you have 4 points to plot so you can sketch the curve.
Example 2: Zeros: 0, 2, and -1/3 so
x = 0, x = 2, and x = -1/3
f (x) = (x)(x - 2)(3x + 1)
= (x2)(3x + 1)
= 3x3 + x2 - 6x2 - 2x
= 3x3 - 5x2 - 2x
Sketch the graph:
1. Leading Coefficient test - odd and positive so falls to the left and rises to the right
2. Use given zeros which is also the y-intercept
Example 3: zeros: 6 + √ 3 and 6 - √3
Therefore:
x = 6 + √3 and x = 6 - √3
f (x) = (x - 6 - √3)(6 - 6 + √3)
= x2 - 6x + x√3 - 6x + 36 - 6√3 - x√3 + 6√3 - (√3)2
= x2 - 12x + 36 - 3
= x2 - 12x + 33
Example 4: (use grouping)
Zeros: 4, 2 + √7, 2 - √7
f (x) = (x - 4)(x - 2 - √7)(x - 2 + √7)
= (x - 4)(x2 - 2x + x√7 - 2x + 4 - 2√7 - x√7 + 2√7 - ( √7)2
= (x - 4)(x2 - 4x + 4 - 7 )
= (x - 4)(x2 - 4x - 3)
= x3 - 4x2 - 3x - 4x2 + 16x + 12
= x3 - 8x2 + 13x + 12
II. The Intermediate Value Theorem:
- This theorem helps locate the real zeros of a polynomial function.
Example 1: Find a value x = a where a polynomial function is positive and another x = b where it is negative, you can conclude that the function has at least one real zero between the two values.
f (x) = x3 - 3x2 + 3
1. Using the leading coefficient test, the graph falls left and rises right
2. Finding a couple of points, (0, 3) is one point and (-3, -5) is another point
(0, 3) is above x-axis while (-3, -51) is below the x-axis so there is a real zero between them (the graph crosses the x-axis)
(2, -1) is also below the x-axis so there is a real zero between (0, 3) and (2, -1)
(5, 53) is another point and that is above the x-axis so there is another real zero between (2, -1) and (5, 53).
This tells us that the graph crosses the x-axis in three different places.
Next using the calculator to find the "exact" zeros:
1. In your calculator: y1 = x3 - 3x2 + 3
2. Press 2nd trace, #2 zero
going from the left, go below the x-axis and this will be your lower bound and then above the x-axis, this will be your upper bound, and then guess around the x-axis.
(-.8793852, 0) which was between (-3, 51) and (0, 3)
(1.3472964, 0) which was between (0, 3) and (2, -1)
(2.5320889, 0) which was between (2, -1) and (5, 53)
Example 2: g(x) = (1/8)(x + 1)2 (x - 3)3
1. the highest degree is 5 which is odd and the leading coefficient is positive so the graph falls to the left and rises to the right.
2. There could be 5 different x-intercepts so trying some different points we have
(-2, -15.625), (-1, 0), (0, -3.375), (1, -4), (2, -1.125), (3, 0), (4, 3.125)
From our table, we see that there are only 2 x-intercepts.
Check this algebraically:
0 = (1/8)(x + 1)2(x - 3)3
0 = (1/8)(x + 1)2
0 = x + 1
-1 = x
0 = (x - 3)3
0 = x - 3
3 = x
These are the two points that we found graphically.
You can find extra notes at the following website:
http://scidiv.bcc.ctc.edu/FL/MATH105/sso0202.pdf
I. Graphs of:
Polynomial functions are continuous if -
they have no breaks, holes, or gaps.
Example 1: This graph is continuous
Example 2: Piece-wise functions are not continuous
II. Simple Graphs:
f (x) = xn, where n is greater than zero
1. If n is even, the graph of y = xn touches the axis at the x-intercept.
2. If n is odd, the graph of y = xn crosses the axis at the x-intercept.
III. The Leading Coefficient Test
Given f(x) = anxn + ... + a1x + a0
1. When "n" is odd:
a. If the Leading Coefficient is positive (an is greater than 0), the graph falls to the left and rises to the right.
b. If the Leading Coefficient is negative (an is less than 0), the graph rises to the left and falls to the right.
2. When "n" is even:
a. If the Leading Coefficient is positive (an is greater than 0), the graph rises to the left and right.
b. If the Leading Coefficient is negative (an is less than 0), the graph falls to the left and right.
*This determines ONLY the right and left behavior of the graph!
IV. Zeros of Polynomial Functions:
1. The graph of "f" has at most "n" real zeros.
2. The function has at most n-1 relative extrema (relative minimum or maximums).
Example: Given y = x2
n = 2
so
2 real zeros and (n-1) or 1 minimum
V. Real Zeros:
1. x = a is a zero of the function "f"
2. x = a is a solution of the polynomial equation f (x) = 0
3. (x - a) is a factor of the polynomial f (x)
4. (a, 0) is an x-intercept of the graph of "f".
Example: f (x) = x2 - 8x + 15
0 = x2 - 8x + 15
0 = (x - 5)(x - 3)
x = 5 and x = 3
therefore the zeros are (5, 0) and (3, 0)
x2 so n = 2 so ... there are at least 2 real zeros
graph: a is greater than 0 so this function rises to the left and right.
Example: f (x) = (-3/8) x4 - x3 + 2x2 + 5
Given the zeros:
1. Leading Coefficient = -3/8
2. Leading Degree is 4 so it is even
Therefore the graph falls to the left and the right.
Note: use the calculator to find the intercepts if algebraically not able to at this stage
When you graph the above function:
Maximum: (-2.914851686, 19.68779879)
Zeros: (-4.141946129, 0) and (1.934035914, 0)
Example: f (x) = x3 - 4x
Leading Coefficient = 1
Leading degree is 3 so it is odd
The graph falls to left and rises to the right
0 = x3 - 4x
0 = x (x2 - 4)
0 = x (x + 2)(x - 2)
0 = x, x = -2, and x = 2
Maximum value (-1.15, 3.08)
Minimum value (1.15, -3.08)
VI. Multiplicity for the Factor (x - r)k
In general, a factor of (x - r)k yields a repeated zero x = r of multiplicity k.
1. If k is odd, the graph crosses the x-axis at x = r
2. If k is even, the graph touches (but does not cross) the x-axis at x = r.
Example: f (x) = 4x2 -6x + 9
Find all zeros:
0 = 4x2 - 6x + 9
0 = (2x - 3)(2x - 3)
0 = (2x - 3)2
so we know a zero is (3, 0)
Using #2 above, k = 2 so it is even, therefore the graph touches the x-axis at x = 3
Example 2: Find the x-intercepts and multiplicity of f (x) = 2(x + 2)2(x - 3)
x-intercepts are (-2, 0) and (3, 0) and the mutiplicity of 2.
2.2b Finding a Polynomial with Given Zeros:
I. Finding a Polynomial with given zeros
Example 1: given zeros: -4 and 5
1. For each of the given zeros, form a corresponding factor.
We have: x = -4 and x = 5
f (x) = (x + 4)(x - 5)
= x2 - 5x + 4x - 20
= x2 - x - 20
Now sketch the graph:
1. Apply the Leading Coefficient test
Leading Coefficient is 1 and 1 is positive and the degree is 2 so it is even
Therefore the graph rises to the left and right.
2. Use zeros given: (-4, 0) and (5, 0)
3. Find the y-intercept by letting x = 0
f (0) = -20
4. Find the vertex
x = -b/(2a) = 1/2
f (1/2) = -20.25
So now you have 4 points to plot so you can sketch the curve.
Example 2: Zeros: 0, 2, and -1/3 so
x = 0, x = 2, and x = -1/3
f (x) = (x)(x - 2)(3x + 1)
= (x2)(3x + 1)
= 3x3 + x2 - 6x2 - 2x
= 3x3 - 5x2 - 2x
Sketch the graph:
1. Leading Coefficient test - odd and positive so falls to the left and rises to the right
2. Use given zeros which is also the y-intercept
Example 3: zeros: 6 + √ 3 and 6 - √3
Therefore:
x = 6 + √3 and x = 6 - √3
f (x) = (x - 6 - √3)(6 - 6 + √3)
= x2 - 6x + x√3 - 6x + 36 - 6√3 - x√3 + 6√3 - (√3)2
= x2 - 12x + 36 - 3
= x2 - 12x + 33
Example 4: (use grouping)
Zeros: 4, 2 + √7, 2 - √7
f (x) = (x - 4)(x - 2 - √7)(x - 2 + √7)
= (x - 4)(x2 - 2x + x√7 - 2x + 4 - 2√7 - x√7 + 2√7 - ( √7)2
= (x - 4)(x2 - 4x + 4 - 7 )
= (x - 4)(x2 - 4x - 3)
= x3 - 4x2 - 3x - 4x2 + 16x + 12
= x3 - 8x2 + 13x + 12
II. The Intermediate Value Theorem:
- This theorem helps locate the real zeros of a polynomial function.
Example 1: Find a value x = a where a polynomial function is positive and another x = b where it is negative, you can conclude that the function has at least one real zero between the two values.
f (x) = x3 - 3x2 + 3
1. Using the leading coefficient test, the graph falls left and rises right
2. Finding a couple of points, (0, 3) is one point and (-3, -5) is another point
(0, 3) is above x-axis while (-3, -51) is below the x-axis so there is a real zero between them (the graph crosses the x-axis)
(2, -1) is also below the x-axis so there is a real zero between (0, 3) and (2, -1)
(5, 53) is another point and that is above the x-axis so there is another real zero between (2, -1) and (5, 53).
This tells us that the graph crosses the x-axis in three different places.
Next using the calculator to find the "exact" zeros:
1. In your calculator: y1 = x3 - 3x2 + 3
2. Press 2nd trace, #2 zero
going from the left, go below the x-axis and this will be your lower bound and then above the x-axis, this will be your upper bound, and then guess around the x-axis.
(-.8793852, 0) which was between (-3, 51) and (0, 3)
(1.3472964, 0) which was between (0, 3) and (2, -1)
(2.5320889, 0) which was between (2, -1) and (5, 53)
Example 2: g(x) = (1/8)(x + 1)2 (x - 3)3
1. the highest degree is 5 which is odd and the leading coefficient is positive so the graph falls to the left and rises to the right.
2. There could be 5 different x-intercepts so trying some different points we have
(-2, -15.625), (-1, 0), (0, -3.375), (1, -4), (2, -1.125), (3, 0), (4, 3.125)
From our table, we see that there are only 2 x-intercepts.
Check this algebraically:
0 = (1/8)(x + 1)2(x - 3)3
0 = (1/8)(x + 1)2
0 = x + 1
-1 = x
0 = (x - 3)3
0 = x - 3
3 = x
These are the two points that we found graphically.
Precalculus 2.1 Quadratic Functions
Precalculus 2.1 Quadratic Functions
2.1 Quadratic Functions
You can find extra notes on this website:
http://scidiv.bcc.ctc.edu/FL/MATH105/sso0201.pdf
I. Quadratic Functions
Definition: Let “n” be a non-negative integer and let an, an-1, …, a2, a1, a0
be real numbers with an ≠ 0.
The Function
f (x) = anxn + an-1xn-1 + … + a2x2 + a1x + a0
is called a POLYNOMIAL FUNCTION of x with degree “n”
Polynomial functions are classified by degree:
f (x) = a is a constant function
f (x) = mx + b is a linear function
f (x) = ax2 + bx + c is a quadratic function where a ≠ 0 and {a, b, c } is contained in the set of Real Numbers
Parabola – a graph of a quadratic function is a special type of u-shaped curve.

Since this graph opens upward, given f (x) = ax2 + bx + c, "a" is greater than 0.
if "a" is less than 0, then the parabola is opened downward.
Vertex is the turning point and the axis of symmetry is perpendicular through the x-value of the vertex. Can be found by x = -b/(2a)
Key: using f(x) = ax2
if "a" is greater than 1, the graph is a vertical stretch of the graph y= f(x)
if 0 is less than "a" which is less than 1, the graph is a vertical shrink of the graph y = f(x)
Standard Form of a Quadratic Function:
f(x) = a (x - h)2 + k, where a ≠ 0,
the axis of symmetry is the vertical line x = h, and the vertex of the function is (h, k)
Example 1: Given the vertex (4, -1) and the point (2, 3), what is the equation of the quadratic function.
y = a (x - h)2 + k
3 = a (2 - 4)2 + (-1)
4 = a (-2)2
4 = a (4)
1 = a
y = 1 (x - 4)2 - 1
Example 2: Given the vertex is (5/2, -3/4) and a point (-2, 4), what is the equation of the quadratic function.
y = a(x - h)2 + k
4 = a(-2 - 5/2)2 + (-3/4)
4.75 = a(-4.5)2
4.75 = 20.25 a
19/81 = a
y = (19/81)(x - 5/2)2 - 3/4
II. Maximum or Minimum values:
To find the maximum or minimum, find the vertex by using
x = -b/(2a)
Example: Given C = 800 - 10x + 0.25 x2
find the minimum cost and the number of fixtures:
x = -b/(2a) = 10/((2)(.25) = 10/.5 = 20
therefore there will be 20 fixtures
C = .25 (20)2 - 10(20) + 800
C = 700
So the minimum cost is $700
You can check by graphing, and the minimum point is (20, 700)
III. Identify the vertex and the intercepts Algebraically.
f(x) = x2 + 9x + 8
Vertex is x=-b/2a = -9/2 = -4.5
f (-9) = (-4.5)2 + 9(-4.5) + 8
= 20.25 - 40.5 + 8
= -12.75
vertex is (-4.5, -12.25)
Intercepts:
Let x = 0
f (0) = 02 + 9(0) + 8 = 8
(0, 8)
Let y = 0
0 = x2 + 9x + 8
0 = (x + 8)(x + 1)
x = -8 and x = -1
so
(-8, 0) and (-1, 0)
IV. Find the equation of a quadratic
Given the two x-intercepts (-2, 0) and (10, 0), can you find the equation?
A. if the parabola opens upward, "a" is greater than 0,
y = a (x - p)(x - q)
because there can be lots of answers depending upon what the value of "a", so we will
Let a = 1
f (x) = (x - (-2))(x - 10)
= (x + 2)(x - 10)
= x2 - 10x + 2x - 20
= x2 - 8x - 20
B. if the parabola opens downward, "a" is less than 0,
y - a (x - p)(x - q)
because again, there can be lots of answers depending upon what the value of "a", so we will
Let a = -1
f(x) = -(x + 2)(x - 10)
= -(x2- 8x - 20)
= -x2 + 8x + 20
2.1 Quadratic Functions
You can find extra notes on this website:
http://scidiv.bcc.ctc.edu/FL/MATH105/sso0201.pdf
I. Quadratic Functions
Definition: Let “n” be a non-negative integer and let an, an-1, …, a2, a1, a0
be real numbers with an ≠ 0.
The Function
f (x) = anxn + an-1xn-1 + … + a2x2 + a1x + a0
is called a POLYNOMIAL FUNCTION of x with degree “n”
Polynomial functions are classified by degree:
f (x) = a is a constant function
f (x) = mx + b is a linear function
f (x) = ax2 + bx + c is a quadratic function where a ≠ 0 and {a, b, c } is contained in the set of Real Numbers
Parabola – a graph of a quadratic function is a special type of u-shaped curve.

Since this graph opens upward, given f (x) = ax2 + bx + c, "a" is greater than 0.
if "a" is less than 0, then the parabola is opened downward.
Vertex is the turning point and the axis of symmetry is perpendicular through the x-value of the vertex. Can be found by x = -b/(2a)
Key: using f(x) = ax2
if "a" is greater than 1, the graph is a vertical stretch of the graph y= f(x)
if 0 is less than "a" which is less than 1, the graph is a vertical shrink of the graph y = f(x)
Standard Form of a Quadratic Function:
f(x) = a (x - h)2 + k, where a ≠ 0,
the axis of symmetry is the vertical line x = h, and the vertex of the function is (h, k)
Example 1: Given the vertex (4, -1) and the point (2, 3), what is the equation of the quadratic function.
y = a (x - h)2 + k
3 = a (2 - 4)2 + (-1)
4 = a (-2)2
4 = a (4)
1 = a
y = 1 (x - 4)2 - 1
Example 2: Given the vertex is (5/2, -3/4) and a point (-2, 4), what is the equation of the quadratic function.
y = a(x - h)2 + k
4 = a(-2 - 5/2)2 + (-3/4)
4.75 = a(-4.5)2
4.75 = 20.25 a
19/81 = a
y = (19/81)(x - 5/2)2 - 3/4
II. Maximum or Minimum values:
To find the maximum or minimum, find the vertex by using
x = -b/(2a)
Example: Given C = 800 - 10x + 0.25 x2
find the minimum cost and the number of fixtures:
x = -b/(2a) = 10/((2)(.25) = 10/.5 = 20
therefore there will be 20 fixtures
C = .25 (20)2 - 10(20) + 800
C = 700
So the minimum cost is $700
You can check by graphing, and the minimum point is (20, 700)
III. Identify the vertex and the intercepts Algebraically.
f(x) = x2 + 9x + 8
Vertex is x=-b/2a = -9/2 = -4.5
f (-9) = (-4.5)2 + 9(-4.5) + 8
= 20.25 - 40.5 + 8
= -12.75
vertex is (-4.5, -12.25)
Intercepts:
Let x = 0
f (0) = 02 + 9(0) + 8 = 8
(0, 8)
Let y = 0
0 = x2 + 9x + 8
0 = (x + 8)(x + 1)
x = -8 and x = -1
so
(-8, 0) and (-1, 0)
IV. Find the equation of a quadratic
Given the two x-intercepts (-2, 0) and (10, 0), can you find the equation?
A. if the parabola opens upward, "a" is greater than 0,
y = a (x - p)(x - q)
because there can be lots of answers depending upon what the value of "a", so we will
Let a = 1
f (x) = (x - (-2))(x - 10)
= (x + 2)(x - 10)
= x2 - 10x + 2x - 20
= x2 - 8x - 20
B. if the parabola opens downward, "a" is less than 0,
y - a (x - p)(x - q)
because again, there can be lots of answers depending upon what the value of "a", so we will
Let a = -1
f(x) = -(x + 2)(x - 10)
= -(x2- 8x - 20)
= -x2 + 8x + 20
Tuesday, September 25, 2007
Precalculus Chapter 1.1b + 1.2a
Chapter 1.1b Functions + 1.2a Graphs of Functions
I. Application: A right triangle is formed in the first quadrant by the x-axis and y-axis and a line through the point (2, 1). Write the area of the triangle as a function of “x”, and determine the domain of the function.
1. Graph the triangle:
- one side of the triangle is the x-axis and another side is the y-axis. Since we do not know exactly where the points of the third line cross the 2 axes, we use the points (0,y) and (x,0).
A = ½ (base)(height) = ½ xy
Since (0, y) , (2, 1) and (x, 0) all lie on the same line, the slopes between any pairs of points are equal.
M = (1 – y)/(2 – 0) = (1 – 0)/(2 – x)
1 – y = 2/(2 – x)
y = -2/ ( 2 – x) + 1
y = (-2 + (2 – x))/ (2 – x)
y = -x / (2 – x)
y = x / (x – 2)
Now using substitution:
A = ½ x (x / (x – 2)) = x2/(2x – 4)
The domain is (2, ∞ ) since the area has to be greater than zero.
II. Evaluating a Difference Quotient:
If f (x) = 2x, then using the difference quotient below

Using f(x) = 2x, plug into the equation above:

2h/h = 2
Example 2: Given 5x – x2,

I. Application: A right triangle is formed in the first quadrant by the x-axis and y-axis and a line through the point (2, 1). Write the area of the triangle as a function of “x”, and determine the domain of the function.
1. Graph the triangle:
- one side of the triangle is the x-axis and another side is the y-axis. Since we do not know exactly where the points of the third line cross the 2 axes, we use the points (0,y) and (x,0).
A = ½ (base)(height) = ½ xy
Since (0, y) , (2, 1) and (x, 0) all lie on the same line, the slopes between any pairs of points are equal.
M = (1 – y)/(2 – 0) = (1 – 0)/(2 – x)
1 – y = 2/(2 – x)
y = -2/ ( 2 – x) + 1
y = (-2 + (2 – x))/ (2 – x)
y = -x / (2 – x)
y = x / (x – 2)
Now using substitution:
A = ½ x (x / (x – 2)) = x2/(2x – 4)
The domain is (2, ∞ ) since the area has to be greater than zero.
II. Evaluating a Difference Quotient:
If f (x) = 2x, then using the difference quotient below

Using f(x) = 2x, plug into the equation above:

2h/h = 2
Example 2: Given 5x – x2,

-5 – h , where h cannot equal zero
Example 3:

Increasing, Decreasing, and Constant Functions
A function “f” is increasing on an interval if, for any x1 and x2 in the interval, when x1 is less than x2 implies that f (x1 ) is less than f(x2 )
A function “f” is decreasing on an interval if, for any x1 and x2 in the interval, when x1 is less than x2 implies that f (x1 ) is greater than f(x2 )
A function “f” is constant on an interval if, for any x1 and x2 in the interval, f (x1 ) = f(x2 )
Check out this website:
http://www.mathematicshelpcentral.com/lecture_notes/precalculus_algebra_folder/increasing_and_decreasing_functions.htm
Example 3:

Increasing, Decreasing, and Constant Functions
A function “f” is increasing on an interval if, for any x1 and x2 in the interval, when x1 is less than x2 implies that f (x1 ) is less than f(x2 )
A function “f” is decreasing on an interval if, for any x1 and x2 in the interval, when x1 is less than x2 implies that f (x1 ) is greater than f(x2 )
A function “f” is constant on an interval if, for any x1 and x2 in the interval, f (x1 ) = f(x2 )
Check out this website:
http://www.mathematicshelpcentral.com/lecture_notes/precalculus_algebra_folder/increasing_and_decreasing_functions.htm
Relative Minimum and Relative Maximum:
1. A function value f (a) is called a relative minimum of “f” if there exists an interval that contains a such that:
1. A function value f (a) is called a relative minimum of “f” if there exists an interval that contains a such that:

So you can see that the function is increasing from (- ∞ , -3) and then again from (2, ∞). The function is decreasing from (-3, 2)
Now lets see an example of relative minimum and relative maximum points:

So you can see that the function's relative minimum point from ( - ∞, 0 ) is
"a" while its relative minimum point from ( 0, ∞) is "c" . The relative maximum point is "b".
Tuesday, September 18, 2007
Precalculus Chapter 1.1a Functions
Precalculus Chapter 1.1 Functions and their Graphs
Definition of a Function: A function “f” from a Set A to a Set B is a relation that assigns to each element “x” in the set A exactly one element “y” in the Set B. The Set A is the domain (or set of inputs) of the function “f”, and the Set B contains the range (or set of outputs).
Example:
Set A contains {1, 2, 3, 4, 5} and Set B contains {a, b, c, d, e }
c) 42 + 3y2 = 6
3y2 = -4x2 - 6
y2 = (1/3)( -4x2 - 6)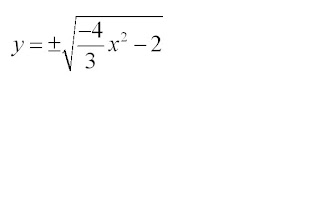
This is not a function!
2). Vertical line test – graph the equation. If you can draw a vertical line and it only touches the graph of the equation once, then the equation is a function. If it touches two or more points, then it is not a function.
3) Function Notation:
Input = x
Output was y, it will now be f(x)
Equation example:
Was: y = 2x + 3
Will now be represented by: f (x) = 2x + 3
EVALUATING A FUNCTION:
Example: f (x) = 2x – 3
f ( 1) = 2 (1) – 3 = 2 – 3 = -1
f (-3) = 2 (-3) – 3 = -6 – 3 = - 9
f (x – 1) = 2 (x – 1) – 3 = 2x – 2 – 3 = 2x – 5
Example: g (y) = 7 – 3y
a. g (0) = 7 – 3(0) = 7
b. g (7/3) = 7 – 3 (7/3) = 7 – 7 = 0
c. g ( s + 2) = 7 – 3 (s + 2 ) = 7 – 3s – 6 = 1 – 3s
A PIECEWISE-DEFINED FUNCTION
- this means that the function is defined by two or more equations over a specified domain.
f (x ) =
Definition of a Function: A function “f” from a Set A to a Set B is a relation that assigns to each element “x” in the set A exactly one element “y” in the Set B. The Set A is the domain (or set of inputs) of the function “f”, and the Set B contains the range (or set of outputs).
Example:
Set A contains {1, 2, 3, 4, 5} and Set B contains {a, b, c, d, e }
Let's say that Set A maps to Set B in giving the following ordered pairs:
{(1, a), (2, c), (3, c), (4, d), (5, b)}
The mapping would look like:
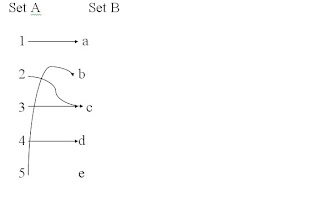
Since every input there is only one output, therefore this is a function.
Remember, for every input there is only one output.
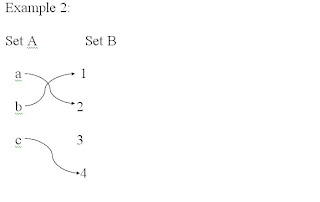
{(a, 2), (b, 1), (c, 4)}
Where a, b, and c are the input and 1, 2, and 4 are the output
CHARACTERISTICS of a FUNCTION:
1). Each element in Set A must be matched with an element of Set B.
2). Some elements in Set B may no be matched with any elements of Set A.
3). Two or more elements of Set A may be matched with the same element of Set B.
FUNCTIONS are commonly represented in four ways:
1). Verbally – by a sentence that describes how the input variable is related to the output variable.
2). Numerically – by a table or list of ordered pairs
3). Graphically
4). Algebraically by an equation in two variables.
example: y = x2 where “y” is a function of “x”
“x” is the independent variable (input or domain)
“y” is the dependent variable (output or range)
TESTING FOR FUNCTION REPRESENTED:
1) Algebraically:
a) 2x + y – 6 = 0 Solve for y.
y = -2x + 6
To each value of “x”, there is only one “y” , therefore this example is a function.
b) 3x2 + 2y = 1
2y = -3x2 + 1
y = (1/2)(-3x2 + 1)
Again, this is a function.
{(1, a), (2, c), (3, c), (4, d), (5, b)}
The mapping would look like:

Since every input there is only one output, therefore this is a function.
Remember, for every input there is only one output.


{(a, 2), (b, 1), (c, 4)}
Where a, b, and c are the input and 1, 2, and 4 are the output
CHARACTERISTICS of a FUNCTION:
1). Each element in Set A must be matched with an element of Set B.
2). Some elements in Set B may no be matched with any elements of Set A.
3). Two or more elements of Set A may be matched with the same element of Set B.
FUNCTIONS are commonly represented in four ways:
1). Verbally – by a sentence that describes how the input variable is related to the output variable.
2). Numerically – by a table or list of ordered pairs
3). Graphically
4). Algebraically by an equation in two variables.
example: y = x2 where “y” is a function of “x”
“x” is the independent variable (input or domain)
“y” is the dependent variable (output or range)
TESTING FOR FUNCTION REPRESENTED:
1) Algebraically:
a) 2x + y – 6 = 0 Solve for y.
y = -2x + 6
To each value of “x”, there is only one “y” , therefore this example is a function.
b) 3x2 + 2y = 1
2y = -3x2 + 1
y = (1/2)(-3x2 + 1)
Again, this is a function.
c) 42 + 3y2 = 6
3y2 = -4x2 - 6
y2 = (1/3)( -4x2 - 6)
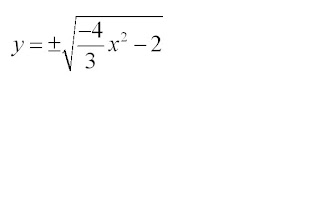
This is not a function!
2). Vertical line test – graph the equation. If you can draw a vertical line and it only touches the graph of the equation once, then the equation is a function. If it touches two or more points, then it is not a function.
3) Function Notation:
Input = x
Output was y, it will now be f(x)
Equation example:
Was: y = 2x + 3
Will now be represented by: f (x) = 2x + 3
EVALUATING A FUNCTION:
Example: f (x) = 2x – 3
f ( 1) = 2 (1) – 3 = 2 – 3 = -1
f (-3) = 2 (-3) – 3 = -6 – 3 = - 9
f (x – 1) = 2 (x – 1) – 3 = 2x – 2 – 3 = 2x – 5
Example: g (y) = 7 – 3y
a. g (0) = 7 – 3(0) = 7
b. g (7/3) = 7 – 3 (7/3) = 7 – 7 = 0
c. g ( s + 2) = 7 – 3 (s + 2 ) = 7 – 3s – 6 = 1 – 3s
A PIECEWISE-DEFINED FUNCTION
- this means that the function is defined by two or more equations over a specified domain.
f (x ) =
{ 2x + 1, x ≤ 0
{ 2x + 2, x is greater than 0
Evaluate: f ( -1)
because -1 is less than 0, we use 2x + 1 so
f (-1) = 2 (-1) + 1 = -2 + 1 = -1
Evaluate: f (0 ) because 0 is equal to 0, we use 2x + 2 so
f (0) = 2x + 2 = 2 (0) + 2 = 2 f (2) = 2x + 2 = 2 (2) + 2 = 4 + 2 = 6
Tuesday, September 11, 2007
Precalculus Prerequisite 5 - Inequalities
Monday, September 10, 2007
Precalculus P4.b Completing the square and
I. Completing the Square:
if x2 + bx = c, then
x2 + bx + (b/2)2 = c + (b/2)2
so:
(x + b/2)2 = c + (b2)/4
Example:
x2 + 4x - 32 = 0
x2 + 4x = 32
therefore b = 4 so:
x2 + 4x + (4/2)2 = 32 + (4/2)2
(x + 2)2 = 32 + 4
(x + 2)2 = 36
take the square root of both sides:
x + 2 = ± √36
x + 2 = ±6
x = -2 ±6
so x = 4 and x = -8
Now check your answers:
(-8)2 + 4(-8) - 32 = 0
64 - 32 - 32 = 0
0 = 0
(4)2 + 4(4) - 32 = 0
16 + 16 - 32 = 0
0 = 0
They both work so our answers are x = 4 and x = -8
Example 2:
x2 - 2x - 3 = 0
x2 - 2x = 3
x2 - 2x + (-2/2)2 = 3 + (-2/2)2
x2 - 2x + (-1)2 = 3 + 1
(x - 1)2 = 4
x - 1 = ±√4
x = 1 ±2
x = 1 + 2 = 3
x = 1 - 2 = -1
check answers:
(3)2 - 2(3) - 3 = 0
9 - 6 - 3 = 0
0 = 0
(-1)2 - 2(-1) - 3 = 0
1 + 2 - 3 = 0
0 = 0
II. Quadratic Formula:
if ax2 + bx + c = 0 then
Example:
9x2 - 12x - 14 = 0
x = (12 ± √(144 - 4(9)(-18)))/(2(9))
x = (12 ± √648)/18
x = (12 ± √324 √2)/18
x = (12 ± 18 √2)/18
x = (2 ± 3 √2)/3
x = 2/3 ± √2
III. Solving an Equation of Quadratic Type:
x4 + 2x3 - 8x - 16 = 0 by grouping
x3 (x + 2) - 8(x + 2) = 0
(x3 - 8 ) ( x + 2) = 0
x3 = 8
x = 2
x + 2 = 0
x = -2
now check the answers:
they both check!
IV. By factoring more difficult equations:
4x2(x - 1)1/3 + 6x (x - 1)4/3 = 0
2x [2x (x - 1)1/3 + 3 (x - 1)4/3] = 0
remember that (x - 1)4/3 = (x - 1) 3/3 (x - 1) 1/3
and 3/3 = 1 so:
2x(x - 1)1/3 [2x + 3 (x - 1)3/3 ] = 0
2x(x - 1)1/3 [ 2x + 3x - 3] = 0
2x(x - 1)1/3 [5x - 3] = 0
so:
2x = 0
x = 0
(x - 1)1/3 = 0
x - 1 = 0
x = 1
5x - 3 = 0
5x = 3
x = 3/5
check your answers!
V. Solving an equation involving a radical:
√(-5x + 4) - x = 6
√(-6x + 4) = x + 6
now square both sides:
(√(-6x + 4))2 = (x + 6)2
-6x + 4 = x2 + 12x + 36
0 = x2 + 18 x + 32
0 = (x + 16)(x + 2)
x = -16 and x = -2
check both answers:
√(-6 (-16) + 4) - (-16) = 6
√(96 + 4 ) + 16 = 6
10 + 16 = 6
not true
√(-6(-2) + 4) - (-2) = 6
√(12 + 4) + 2 = 6
√16 + 2 = 6
4 + 2 = 6
this one works! so
x = -2 is the only answer!
VI. Solving an Equation Involving Two radicals:
√x + √(x - 20) = 10
√ x = 10 - √(x - 20)
(√x)2 = (10 - √(x - 20))2
x = 100 - 20√(x - 20) + (x - 20)
0 = 80 - 20√(x - 20)
-80 = -20√(x - 20)
4 = √(x - 20)
42 = x - 20
16 = x - 20
36 = x
Now check your answer.
√36 + √(36 - 20) = 10
6 + 4 = 10 so it checks
VII. Solving an Equation with Rational Exponents
Example:
(x - 5)2/3 = 16
to undo exponents, multiply by the reciprocal
((x - 5)2/3)3/2 = 163/2
x - 5 = 64
x = 69
Check your answer.
(69 - 5)2/3 = 16
642/3 = 16
16 = 16 so it checks
VIII. Solving an Equation Involving Absolute Value:
recall: |x| = 9
x = 9 and x = -9 so
|3x + 2 | = 7
3x + 2 = 7 and 3x + 2 = -7
3x = 5 and 3x = -9
x = 5/3 and x = -3
Thursday, September 6, 2007
Precalculus Prerequisite 4a - Solving Equations Algebraically and Graphically
Prerequisite 4a - Solving Equations Algebraically and Graphically
I. Vocabulary:
A. An Equation - is a statement that two algebraic expressions are equal.
Example: 2x + 4 = 10
B. To Solve an equation in "x" means to find all values of "x" for which the statement is true. These values are solutions.
Example: 2x + 4 = 10
2x = 6
x = 3
C. An identity equation- an equation that is true for every real number in the domain of the variable.
Example: x2 - 6x + 9 = (x - 3)2
D. Conditional Equation - an equation that is true for just some (or even none of the real numbers in the domain of the variable.
Example 1: x2 - 6x + 9 = 0
(x - 3)2 = 0
x = 3 only
Example 2: 3x + 2 = 4x - 5
x = 7 only
Example 3: x2 + 3x + 4 = 4x - 5
no solutions
E. Notations:
1. all real numbers - R
2. no solutions - { } empty set or Æ is the null set
F. Solving an Equation Involving Fractions:
Example 1: x/4 + (2x)/3 = 6
multiply by the LCD
4, 3 are the denominators so the LCD = 12, so multiply each term by 12:
12(x/4) + (12)(2x)/3 = (12)(6)
3x + 8x = 72
11x = 72
x = 72/11
Example 2: 5/x + (3x)/2 = 7
LCD = 2x
(2x)(5/x) + (2x)(3x)/2 = (2x)(7)
10 + 3x2 = 14x
3x2 - 14 x + 10 = 0
use the quadratic equation
x = (-b ± Ö(b2 - 4ac))/(2a)
x = (14 ± Ö(142 - (4)(3)(10)))/((2)(3))
x = (14 ± Ö76)/3
x = (7 + Ö 19)/3 and x = (7 - Ö19)/3
or
x = 3.786299648 and x = .8803670188 (check to make sure they both work - they do!)
You can also check by using your graphing calculator -
put in
y1 = 5/x + (3x)/2 and
y2 = 7
calc ® intersect, shows the same answers!
G. Extraneous Solutions - an answer or solution that does not satisfy the original equation.
Example:
6/x - 2/(x+3) = (3(x+5))/(x(x + 3))
LCD = x(x+3)
6(x + 3) - 2x = 3(x + 5)
6x + 18 - 2x = 3x + 15
4x + 18 = 3x + 15
x = -3
substituting x=-3 back into the original equation, we have
-2 - 2/0 = 6/0
This is impossible so there is not a solution
H. To find the x-intercepts (a, 0), let y = 0 and solve for x.
To find the y-intercepts (0, b), let x = 0 and solve for y.
Example:
2x2 - 5x + 2 = y
x-intercepts, let y = 0
2x2 - 5x + 2 = 0
(2x -1)(x - 2) = 0
2x - 1 = 0 and x - 2 = 0
x = 1/2 and x = 2
(.5, 0) and (2, 0)
y-intercepts, let x = 0
2(0)2 - 5(0) + 2 = y
2 = y
(0,2)
I. Finding Solutions Graphically:
24x3 - 36x + 17 = 0
graph this on your calculator and you see there is only one solution:
window:
x-values: -10 to 10
y-values: -5 to 40
You can see it is hard to tell how many times the equation crosses the x-axis
so change the y-values to -3 to 3 and you see it crosses y=0 only once
x = -1.414486, y=0
J. Can find answers more than one way, here are a couple using the calculator:
1. y1 = 24x3 - 36x + 17
2nd trace ® zero
enter left-bound before x=-2 and then right-bound after x=-1, then guess about -1.5, gives the answer.
2. y1 = 24x3 - 36x + 17
y2 = 0
2nd trace, #5 intersect, enter 3 times about where the two equations intersect.
K. Remember with points of intersection, always look for all solutions:
Example: 24x3 - 36x + 17 = 2x + 5 has how many solutions?
(-1.393598, 2.212803)
(.3407855, 5.681571)
(1.052813, 7.105626)
remember there can be no points of intersection (therefore no solutions), one solution or many solutions.
L. Solving Polynomial Equations Algebraically:
1. First degree equation - linear equation -
example: 2x + 4 = 7
2. Second degree equation - quadratic equation -
example: 2x2 + 4x + 6 = 0
3. Third degree equation - Cubic equation -
example: 2x3 + 2x2 + 5x + 2 = 0
4. Fourth degree equation - Quartic equation -
example: 2x4 + 3x3 - 2x2 + 3x + 2 = 0
5. Fifth degree equation - Quintic equation -
example: 4x5 + 2x4 - 3x3+ 2x2 + x - 4 = 0
I. Vocabulary:
A. An Equation - is a statement that two algebraic expressions are equal.
Example: 2x + 4 = 10
B. To Solve an equation in "x" means to find all values of "x" for which the statement is true. These values are solutions.
Example: 2x + 4 = 10
2x = 6
x = 3
C. An identity equation- an equation that is true for every real number in the domain of the variable.
Example: x2 - 6x + 9 = (x - 3)2
D. Conditional Equation - an equation that is true for just some (or even none of the real numbers in the domain of the variable.
Example 1: x2 - 6x + 9 = 0
(x - 3)2 = 0
x = 3 only
Example 2: 3x + 2 = 4x - 5
x = 7 only
Example 3: x2 + 3x + 4 = 4x - 5
no solutions
E. Notations:
1. all real numbers - R
2. no solutions - { } empty set or Æ is the null set
F. Solving an Equation Involving Fractions:
Example 1: x/4 + (2x)/3 = 6
multiply by the LCD
4, 3 are the denominators so the LCD = 12, so multiply each term by 12:
12(x/4) + (12)(2x)/3 = (12)(6)
3x + 8x = 72
11x = 72
x = 72/11
Example 2: 5/x + (3x)/2 = 7
LCD = 2x
(2x)(5/x) + (2x)(3x)/2 = (2x)(7)
10 + 3x2 = 14x
3x2 - 14 x + 10 = 0
use the quadratic equation
x = (-b ± Ö(b2 - 4ac))/(2a)
x = (14 ± Ö(142 - (4)(3)(10)))/((2)(3))
x = (14 ± Ö76)/3
x = (7 + Ö 19)/3 and x = (7 - Ö19)/3
or
x = 3.786299648 and x = .8803670188 (check to make sure they both work - they do!)
You can also check by using your graphing calculator -
put in
y1 = 5/x + (3x)/2 and
y2 = 7
calc ® intersect, shows the same answers!
G. Extraneous Solutions - an answer or solution that does not satisfy the original equation.
Example:
6/x - 2/(x+3) = (3(x+5))/(x(x + 3))
LCD = x(x+3)
6(x + 3) - 2x = 3(x + 5)
6x + 18 - 2x = 3x + 15
4x + 18 = 3x + 15
x = -3
substituting x=-3 back into the original equation, we have
-2 - 2/0 = 6/0
This is impossible so there is not a solution
H. To find the x-intercepts (a, 0), let y = 0 and solve for x.
To find the y-intercepts (0, b), let x = 0 and solve for y.
Example:
2x2 - 5x + 2 = y
x-intercepts, let y = 0
2x2 - 5x + 2 = 0
(2x -1)(x - 2) = 0
2x - 1 = 0 and x - 2 = 0
x = 1/2 and x = 2
(.5, 0) and (2, 0)
y-intercepts, let x = 0
2(0)2 - 5(0) + 2 = y
2 = y
(0,2)
I. Finding Solutions Graphically:
24x3 - 36x + 17 = 0
graph this on your calculator and you see there is only one solution:
window:
x-values: -10 to 10
y-values: -5 to 40
You can see it is hard to tell how many times the equation crosses the x-axis
so change the y-values to -3 to 3 and you see it crosses y=0 only once
x = -1.414486, y=0
J. Can find answers more than one way, here are a couple using the calculator:
1. y1 = 24x3 - 36x + 17
2nd trace ® zero
enter left-bound before x=-2 and then right-bound after x=-1, then guess about -1.5, gives the answer.
2. y1 = 24x3 - 36x + 17
y2 = 0
2nd trace, #5 intersect, enter 3 times about where the two equations intersect.
K. Remember with points of intersection, always look for all solutions:
Example: 24x3 - 36x + 17 = 2x + 5 has how many solutions?
(-1.393598, 2.212803)
(.3407855, 5.681571)
(1.052813, 7.105626)
remember there can be no points of intersection (therefore no solutions), one solution or many solutions.
L. Solving Polynomial Equations Algebraically:
1. First degree equation - linear equation -
example: 2x + 4 = 7
2. Second degree equation - quadratic equation -
example: 2x2 + 4x + 6 = 0
3. Third degree equation - Cubic equation -
example: 2x3 + 2x2 + 5x + 2 = 0
4. Fourth degree equation - Quartic equation -
example: 2x4 + 3x3 - 2x2 + 3x + 2 = 0
5. Fifth degree equation - Quintic equation -
example: 4x5 + 2x4 - 3x3+ 2x2 + x - 4 = 0
Subscribe to:
Posts (Atom)













