1. Δ ABC is congruent to Δ ABC , this is by the Reflexive Postulate
2. if Δ ABC is congruent to Δ DEF then Δ DEF is congruent to Δ ABC, this is by the Symmetric Postulate
3. if Δ ABC is congruent to Δ DEF and Δ DEF is congruent to Δ GHI, Then Δ ABC is congruent to Δ GHI by the Transitivity Postulate
5 ways to show Triangle Congruence:
1. SAS = SAS Congruence Postulate - if two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the two triangles are congruent.
Example: Given ΔABC and ΔDEF,
if AB = DE, BC = EF and angle B = angle E, then ΔABC = ΔDEF.
2. SSS = SSS Congruence Postulate - if three sides of one triangle are congruent to three sides of a second triangle, then the two triangles are congruent.
Example: Given ΔABC and ΔDEF,
if AB = DE, BC = EF and AC = DF, then ΔABC = ΔDEF.
3. ASA = ASA Congruence Postulate - if two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the two triangles are congruent.
Example: Given ΔABC and ΔDEF,
if angle A = angle D, AB = DE, and angle B = angle E, then Δ ABC = Δ DEF.
4. AAS = AAS Congruence Postulate - if two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of a second triangle, then the two triangles are congruent.
Example: Given Δ ABC and Δ DEF,
if angle A = angle D, angle C = angle F, and BC = EF , then Δ ABC = Δ DEF.
5. HL = HL Congruence Postulate - if the leg and hypotenuse of one right triangle is congruent to the corresponding leg and hypotenuse of another right triangle, then the two triangles are congruent by hypotenuse - leg postulate.
Example: Given right Δ ABC and right Δ DEF, if angle B and angle E are both right angles and leg AB = leg DE and hypotenuse AC = hypotenuse DF, then Δ ABC = Δ DEF.
I) Vocabulary:
A) When two figures are congruent, there is a correspondence between their angles and sides such that corresponding angles are congruent and corresponding sides are congruent.
Example: Given Δ ABC is congruent to Δ PQR then we know
1) angle A = angle P, angle B = angle Q, and angle C = angle R
2) AB = PQ, BC = QR, and AC = PR By Corresponding Parts of Congruent Triangles are Congruent (CPCTC) - which means that if 2 triangles are congruent, then their corresponding parts are congruent
Make sure that you list the corresponding angles in the same order with the triangle congruence.
Example: ΔABC = ΔDEF is not the same as ΔABC = ΔEFD because
ΔABC = ΔDEF has angle A = angle D, angle B = angle E and angle C = angle F
while ΔABC = ΔEFD has angle A = angle E, angle B = angle F and angle C = angle D
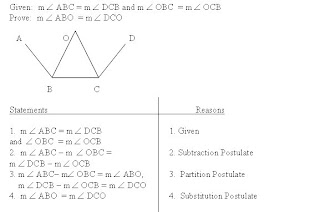
B) Third Angles Theorem - if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.
C) Reflexive Postulate - Every triangle is congruent to itself
D) Symmetric Postulate - If ΔABC = ΔDEF, then ΔDEF = ΔABC
E) Transitive Postulate - If ΔABC = ΔDEF and ΔDEF = ΔJKL, then ΔABC = ΔJKL
Theorems to remember:
If 2 angles of one triangle are congruent then the sides opposite are congruent.
If 2 sides of one triangle are congruent then the angles opposite are congruent.
________________________________________________________________
Practice Proofs: