Definition of a Function: A function “f” from a Set A to a Set B is a relation that assigns to each element “x” in the set A exactly one element “y” in the Set B. The Set A is the domain (or set of inputs) of the function “f”, and the Set B contains the range (or set of outputs).
Example:
Set A contains {1, 2, 3, 4, 5} and Set B contains {a, b, c, d, e }
Let's say that Set A maps to Set B in giving the following ordered pairs:
{(1, a), (2, c), (3, c), (4, d), (5, b)}
The mapping would look like:
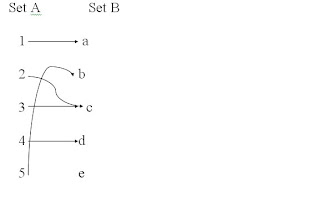
Since every input there is only one output, therefore this is a function.
Remember, for every input there is only one output.
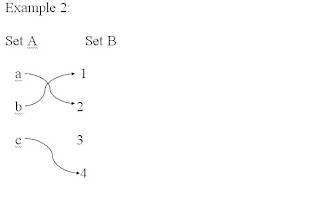
{(a, 2), (b, 1), (c, 4)}
Where a, b, and c are the input and 1, 2, and 4 are the output
CHARACTERISTICS of a FUNCTION:
1). Each element in Set A must be matched with an element of Set B.
2). Some elements in Set B may no be matched with any elements of Set A.
3). Two or more elements of Set A may be matched with the same element of Set B.
FUNCTIONS are commonly represented in four ways:
1). Verbally – by a sentence that describes how the input variable is related to the output variable.
2). Numerically – by a table or list of ordered pairs
3). Graphically
4). Algebraically by an equation in two variables.
example: y = x2 where “y” is a function of “x”
“x” is the independent variable (input or domain)
“y” is the dependent variable (output or range)
TESTING FOR FUNCTION REPRESENTED:
1) Algebraically:
a) 2x + y – 6 = 0 Solve for y.
y = -2x + 6
To each value of “x”, there is only one “y” , therefore this example is a function.
b) 3x2 + 2y = 1
2y = -3x2 + 1
y = (1/2)(-3x2 + 1)
Again, this is a function.
{(1, a), (2, c), (3, c), (4, d), (5, b)}
The mapping would look like:

Since every input there is only one output, therefore this is a function.
Remember, for every input there is only one output.


{(a, 2), (b, 1), (c, 4)}
Where a, b, and c are the input and 1, 2, and 4 are the output
CHARACTERISTICS of a FUNCTION:
1). Each element in Set A must be matched with an element of Set B.
2). Some elements in Set B may no be matched with any elements of Set A.
3). Two or more elements of Set A may be matched with the same element of Set B.
FUNCTIONS are commonly represented in four ways:
1). Verbally – by a sentence that describes how the input variable is related to the output variable.
2). Numerically – by a table or list of ordered pairs
3). Graphically
4). Algebraically by an equation in two variables.
example: y = x2 where “y” is a function of “x”
“x” is the independent variable (input or domain)
“y” is the dependent variable (output or range)
TESTING FOR FUNCTION REPRESENTED:
1) Algebraically:
a) 2x + y – 6 = 0 Solve for y.
y = -2x + 6
To each value of “x”, there is only one “y” , therefore this example is a function.
b) 3x2 + 2y = 1
2y = -3x2 + 1
y = (1/2)(-3x2 + 1)
Again, this is a function.
c) 42 + 3y2 = 6
3y2 = -4x2 - 6
y2 = (1/3)( -4x2 - 6)
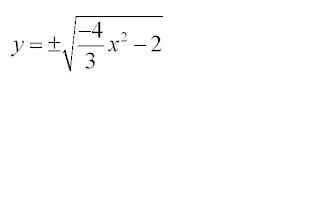
This is not a function!
2). Vertical line test – graph the equation. If you can draw a vertical line and it only touches the graph of the equation once, then the equation is a function. If it touches two or more points, then it is not a function.
3) Function Notation:
Input = x
Output was y, it will now be f(x)
Equation example:
Was: y = 2x + 3
Will now be represented by: f (x) = 2x + 3
EVALUATING A FUNCTION:
Example: f (x) = 2x – 3
f ( 1) = 2 (1) – 3 = 2 – 3 = -1
f (-3) = 2 (-3) – 3 = -6 – 3 = - 9
f (x – 1) = 2 (x – 1) – 3 = 2x – 2 – 3 = 2x – 5
Example: g (y) = 7 – 3y
a. g (0) = 7 – 3(0) = 7
b. g (7/3) = 7 – 3 (7/3) = 7 – 7 = 0
c. g ( s + 2) = 7 – 3 (s + 2 ) = 7 – 3s – 6 = 1 – 3s
A PIECEWISE-DEFINED FUNCTION
- this means that the function is defined by two or more equations over a specified domain.
f (x ) =
{ 2x + 1, x ≤ 0
{ 2x + 2, x is greater than 0
Evaluate: f ( -1)
because -1 is less than 0, we use 2x + 1 so
f (-1) = 2 (-1) + 1 = -2 + 1 = -1
Evaluate: f (0 ) because 0 is equal to 0, we use 2x + 2 so
f (0) = 2x + 2 = 2 (0) + 2 = 2 f (2) = 2x + 2 = 2 (2) + 2 = 4 + 2 = 6