Precalculus 1.2 b Graphs of functions:
I. to graph a piece-wise function:
Given:
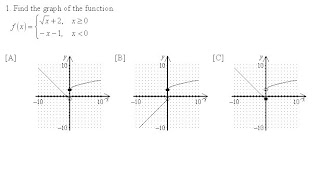
So to find the answer to this, find f(0).
Since 0 is equal to 0, we would use the first function.
so f(0) = √0 + 2 = 2, this means it is a solid dot at (0, 2) so the answer cannot be C.
and it is an open dot at f(0) = -x - 1 = -1 because it does not equal zero here.
Now we look at the graph of each function.
f(x) = -x - 1 has a negative slope so the answer would be A.
A way to check your answer is by using your graphing utility.
In y1 = (√ x + 2)(x≥0)
In y2 = (- x - 1)(x is less than 0)
with this you can see that the graph could be A or C. Now using your table, you can see that
y1 = 2 where y2 = 0 (this zero means no - the function doesn't exist here) so this means that
y1 would be a solid dot and y2 is open.
II. Even Function:
A function f is even if, for each x in the domain of f, f (-x) = f (x)
Example:
f (x) = x2 + 4
Test the function:
1st - Is it a function - yes it is
2nd - does f (-x) = f (x)
f (-x) = (-x)2 + 4
= x2 + 4
Therefore: f (-x) = x2 + 4 and
f (x) = x2 so
f (-x) = f (x) so this function is even.
III. Odd Function
A function f is odd if, for each x in the domain of f,
f (-x) = - f (x)
Example:
f(x) = x5 - x3
f(-x) = (-x)5 - (-x)3
= -x5 - - x3
= - (x5 - x3)
-f(x) = - (x5 - x3) so...
f (-x) = - f(x) so this function is odd.
IV. Neither an Even Function or Odd Function
A function f is neither if, for each x in the domain of f
a) f (-x) ≠ f (x) AND
b) f (-x) ≠ - f(x)
Example:
f (x) = 5 - 3x
f (-x) = 5 - 3(-x) = 5 + 3x
-f(x) = - (5 - 3x) = -5 + 3x
so since f (x) ≠ f (-x) and
f (-x) ≠ - f(x), this function is neither even or odd
V. Graphically showing even, odd or neither functions:

I. to graph a piece-wise function:
Given:

So to find the answer to this, find f(0).
Since 0 is equal to 0, we would use the first function.
so f(0) = √0 + 2 = 2, this means it is a solid dot at (0, 2) so the answer cannot be C.
and it is an open dot at f(0) = -x - 1 = -1 because it does not equal zero here.
Now we look at the graph of each function.
f(x) = -x - 1 has a negative slope so the answer would be A.
A way to check your answer is by using your graphing utility.
In y1 = (√ x + 2)(x≥0)
In y2 = (- x - 1)(x is less than 0)
with this you can see that the graph could be A or C. Now using your table, you can see that
y1 = 2 where y2 = 0 (this zero means no - the function doesn't exist here) so this means that
y1 would be a solid dot and y2 is open.
II. Even Function:
A function f is even if, for each x in the domain of f, f (-x) = f (x)
Example:
f (x) = x2 + 4
Test the function:
1st - Is it a function - yes it is
2nd - does f (-x) = f (x)
f (-x) = (-x)2 + 4
= x2 + 4
Therefore: f (-x) = x2 + 4 and
f (x) = x2 so
f (-x) = f (x) so this function is even.
III. Odd Function
A function f is odd if, for each x in the domain of f,
f (-x) = - f (x)
Example:
f(x) = x5 - x3
f(-x) = (-x)5 - (-x)3
= -x5 - - x3
= - (x5 - x3)
-f(x) = - (x5 - x3) so...
f (-x) = - f(x) so this function is odd.
IV. Neither an Even Function or Odd Function
A function f is neither if, for each x in the domain of f
a) f (-x) ≠ f (x) AND
b) f (-x) ≠ - f(x)
Example:
f (x) = 5 - 3x
f (-x) = 5 - 3(-x) = 5 + 3x
-f(x) = - (5 - 3x) = -5 + 3x
so since f (x) ≠ f (-x) and
f (-x) ≠ - f(x), this function is neither even or odd
V. Graphically showing even, odd or neither functions:
1. A function whose graph is symmetric with respect to the y-axis is an even function.
2. A function whose graph is symmetric with respect to the origin is an odd function.
3. A function whose graph is not symmetric with respect to the y-axis or the origin is a neither function.
Example:
Can you figure out which of these graphs are even, odd or neither?

1. Graph A is neither because it is not symmetric to the y-axis or the origin.
2. Graph B is an even function because it is symmetric to the y-axis.
3. Graph C is an odd function because it is symmetric to the origin.
VI. The Greatest Interger Function:
is denoted by [[x]] and is defined by
f (x) = [[x]] = the greatest integer less than or equal to x.
The graph of the greatest integer function jumps vertically one unit at each integer and is contant (a horizontal line segment) between each pair of consecutive integers.
Example: f (x) = [[x]]
[[-2]] = -2
[[-1.5]] = -2
[[-0.5]] = -1
[[1.5]] = 1
From this you can see that the value of the x rounded down to the nearest integer.
To put this on the graphing utility:
y1 = math → num↓#5 int( x)
Example 2:
f (-4) = [[-1]] - 2 = -1 - 2 = -3
f (-3.5) = [[-.875]] - 2 = -1 - 2 = -3
So we can definitely throw C away. So looking at A or B,
and since f (-4) = -3, this means the dot is closed so the answer would be A.
