Geometry - Similar Triangle Proofs

Similar Triangle Proofs:

If 2 angles of one triangle are congruent to two corresponding angles of a second triangle, then the third angles are congruent.

There are 3 ways to show triangle similarity:



Let's try a proof:

Let's try another:

Geometry HW #14

For my Geometry Class: here is homework #14, questions 1 & 2 Quadrilateral Proofs

Quadrialteral Properties

Quadrilateral "Family Tree" -

Quadrilateral - 4 sided polygon

A. Kite -
1. has consecutive sides congruent but opposite sides are not.
2. the diagonals are perpendicular
3. has exactly one pair of opposite angles congruent.

B. Trapezoid -
1. Has exactly one pair of opposite sides parallel

C. Isosceles Trapezoid -
1. Has exactly one pair of opposite sides parallel
2. the non-parallel sides are congruent (legs congruent)
3. the diagonals are congruent
4. the base angles are congruent

D. Parallelogram -
1. Definition: has both pairs of opposite sides parallel
2. has both pairs of opposite sides congruent
3. has one pair of opposite sides parallel and congruent
4. has both pairs of opposite angles congruent
5. has consecutive angles supplementary
6. the diagonals bisect each other
7. the diagonals divide the parallelogram into 2 congruent triangles

E. Rhombus -
1. All of the properties of a parallelogram
2. All sides are congruent (equilateral)
3. diagonals are perpendicular
4. diagonals bisect opposite angles

F. Rectangle -
1. All of the properties of a parallelogram
2. all angles are congruent (equiangular)
3. diagonals are congruent

G. Square -
1. All the properties of a parallelogram, rhombus and rectangle

check out this website:
http://regentsprep.org/Regents/math/quad/LQuad.htm

Coordinate Geometry

Geometry - Coordinate Geometry:

check out this website:
http://regentsprep.org/Regents/mathb/1D/Coordinatelesson.htm

B(x₁, y₁) and A (x₂, y₂) is from the
Pythagorean Theorem which is:

c² = a² + b²

since a = (x₂ – x₁) and b = (y₂ – y₁)

we get

c² = (x₂ – x₁)² + (y₂ – y₁)²
so taking the square root of both sides we have our distance formula.

Here are the Slope Formula and the Midpoint Formula:

Using the following chart, if we have to prove congruent segments, we have to show they have equal length by using the distance formula.

Here is a web-site to hopefully help:

http://library.thinkquest.org/20991/geo/coordgeo.html

Geometry Proofs - unit 2 Triangles

Triangles – Proofs – Unit 2
1. Δ ABC is congruent to Δ ABC , this is by the Reflexive Postulate
2. if Δ ABC is congruent to Δ DEF then Δ DEF is congruent to Δ ABC, this is by the Symmetric Postulate
3. if Δ ABC is congruent to Δ DEF and Δ DEF is congruent to Δ GHI, Then Δ ABC is congruent to Δ GHI by the Transitivity Postulate

5 ways to show Triangle Congruence:
1. SAS = SAS Congruence Postulate - if two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the two triangles are congruent.
Example: Given ΔABC and ΔDEF,
if AB = DE, BC = EF and angle B = angle E, then ΔABC = ΔDEF.

2. SSS = SSS Congruence Postulate - if three sides of one triangle are congruent to three sides of a second triangle, then the two triangles are congruent.
Example: Given ΔABC and ΔDEF,
if AB = DE, BC = EF and AC = DF, then ΔABC = ΔDEF.

3. ASA = ASA Congruence Postulate - if two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the two triangles are congruent.
Example: Given ΔABC and ΔDEF,
if angle A = angle D, AB = DE, and angle B = angle E, then Δ ABC = Δ DEF.

4. AAS = AAS Congruence Postulate - if two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of a second triangle, then the two triangles are congruent.
Example: Given Δ ABC and Δ DEF,
if angle A = angle D, angle C = angle F, and BC = EF , then Δ ABC = Δ DEF.

5. HL = HL Congruence Postulate - if the leg and hypotenuse of one right triangle is congruent to the corresponding leg and hypotenuse of another right triangle, then the two triangles are congruent by hypotenuse - leg postulate.
Example: Given right Δ ABC and right Δ DEF, if angle B and angle E are both right angles and leg AB = leg DE and hypotenuse AC = hypotenuse DF, then Δ ABC = Δ DEF.

I) Vocabulary:
A) When two figures are congruent, there is a correspondence between their angles and sides such that corresponding angles are congruent and corresponding sides are congruent.
Example: Given Δ ABC is congruent to Δ PQR then we know
1) angle A = angle P, angle B = angle Q, and angle C = angle R
2) AB = PQ, BC = QR, and AC = PR By Corresponding Parts of Congruent Triangles are Congruent (CPCTC) - which means that if 2 triangles are congruent, then their corresponding parts are congruent

Make sure that you list the corresponding angles in the same order with the triangle congruence.
Example: ΔABC = ΔDEF is not the same as ΔABC = ΔEFD because
ΔABC = ΔDEF has angle A = angle D, angle B = angle E and angle C = angle F
while ΔABC = ΔEFD has angle A = angle E, angle B = angle F and angle C = angle D

B) Third Angles Theorem - if two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent.

C) Reflexive Postulate - Every triangle is congruent to itself

D) Symmetric Postulate - If ΔABC = ΔDEF, then ΔDEF = ΔABC

E) Transitive Postulate - If ΔABC = ΔDEF and ΔDEF = ΔJKL, then ΔABC = ΔJKL

Theorems to remember:

If 2 angles of one triangle are congruent then the sides opposite are congruent.
If 2 sides of one triangle are congruent then the angles opposite are congruent.
________________________________________________________________
Practice Proofs:

Precalculus Unit 8 - chapter 6.3, 6.4, 10.5, 10.6, 10.7

PRECALCULUS
Unit 8
Vectors and Parametric/Polar Equations

Section 6.3A HW# 53; Pg.453; #1 – 45 by 4’s (1, 5, 9, …)

Section 6.3B; HW # 54; *Pg.453; #3, 11, 19, 23, 31, 39, 43
Pg.454; #49, 53, 57, 61, 65, 69, 73, 74, 82

Section 6.4; HW # 55; *Pg. 454; #51, 55, 59, 63, 67, 71,
Pg. 464; #1, 5, 9, 13, 17, 21, 25, 29, 33, 37
Quiz on Sections 6.3A – 6.3B Next Class

Section 10.5; HW# 56; *Pg.464; #3, 7, 11, 15, 19, 23, 27, 31
Pg.736; #1, 5, 9, 13, 21, 29, 41, 47

Section 10.6; HW# 57; *Pg.736; #3, 7, 11, 17, 27, 43
Pg.743; #5 – 41 by 4’s, 45, 50, 53 – 57 odds
Quiz on Sections 6.4 – 10.5 Next Class

Section 10.7; HW# 58; *Pg.743; #7, 11, 15, 23, 27, 39, 47, 59
Pg.752; #21 – 33 odds, 55, 59

Review HW #59
Pg.480; 39, 43, 47, 51, 59, 69, 79, 83, 85
Pg.762; 47, 49, 59, 65, 69, 73, 75, 81, 85, 89

HW #60; Unit 8 Test

Unit One for Proofs - Angles and Lines

The addition Postulate:

If a = b and c = d, then a + c = b + d

The Partition Postulate:

AB + BC = AC

These are two different concepts. Let's try a proof:

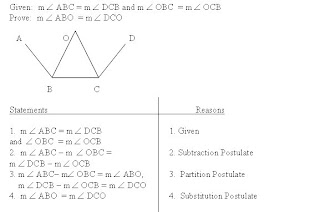
As you can see, in step 2, we added equal quantities to each other. This is Addition Postulate.

But in step 3, we added a part plus a part equals a whole so this is Partition.

Let's try another example:

Here we used the Subtraction Postulate: subtracting equal quantities from equal quantities.

In step 3, we had the whole minus a part equals a part. This is still Partition Postulate.